《2025年课堂点睛八年级数学上册北师大版》

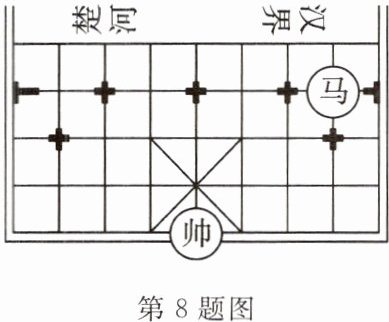
8. (贵州省中考改编)象棋起源于中国,中国象棋文化历史悠久.如图所示是某次对弈的残图,如果建立平面直角坐标系,使棋子“帅”位于点$(-2,-1)$的位置,则在同一坐标系下,经过棋子“帅”和“马”所在的点的一次函数表达式为(A)

A.$y = x + 1$
B.$y = x - 1$
C.$y = 2x + 1$
D.$y = 2x - 1$

答案： A

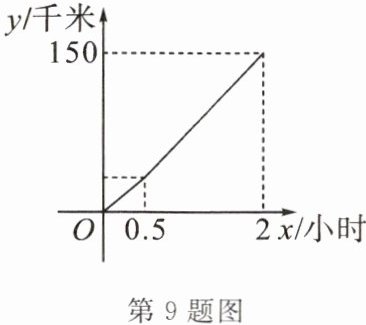
9. (威海市中考)一辆汽车在行驶过程中,其行驶路程$y$(千米)与行驶时间$x$(小时)之间的函数关系如图所示.当$0\leqslant x\leqslant 0.5$时,$y与x之间的函数表达式为y = 60x$；当$0.5\leqslant x\leqslant 2$时,$y与x$之间的函数表达式为y=80x-10.

答案： y=80x-10

10. (跨学科)某地区山峰的高度每增加$1$百米,气温大约降低$0.6^{\circ}C$,气温$T(^{\circ}C)和高度h$(百米)的函数关系如图所示.
请根据图象解决下列问题：
(1)高度为$5$百米时的气温是12℃；
(2)求$T关于h$的函数表达式；
(3)测得某山顶的气温为$6^{\circ}C$,求该山峰的高度.

答案：
(1)12℃
(2)解:设 T 关于 h 的函数表达式为 T=kh+b,则{3k+b=13.2,5k+b=12.解得{k=-0.6,b=15.
∴T 关于 h 的函数表达式为 T=-0.6h+15(h＞0).
(3)当 T=6时,6=-0.6h+15,解得 h=15.
∴该山峰的高度大约为 15 百米,即1500 米.

11. (核心素养·应用意识))随着地球上的水资源日益枯竭,各级政府越来越重视倡导节约用水.某市生活用水按“阶梯水价”方式进行收费,人均月生活用水收费标准如图所示,图中$x$表示人均月生活用水的吨数,$y$表示收取的人均月生活用水的水费(元).请根据图象信息,回答下列问题：
(1)该市人均月生活用水的收费标准是：不超过$5t$,每吨按1.6元收取；超过$5t$的部分,每吨按2.4元收取；
(2)求出$y与x$的函数关系式；
解:当 0≤x≤5时,设 y=kx,则有 5k=8,k=1.6,
∴y=1.6x;当 x＞5 时,设 y=k1x+b,由题意得{5k1+b=8,10k1+b=20,解得{k1=2.4,b=-4,
∴y=2.4x-4.综合以上得 y={1.6x,(0≤x≤5)2.4x-4.(x＞5)
(3)若某个家庭有$5$人,五月份的生活用水的水费共$76$元,则该家庭这个月用了多少吨生活用水?
∵76/5=15.2(元)＞8 元,
∴将 y=15.2 代入 y=2.4x-4 得 x=8,即人均用水为 8 吨,8×5=40(吨).答:该家庭这个月用了 40 吨生活用水.

答案：
(1)1.6 2.4
(2)解:当 0≤x≤5时,设 y=kx,则有 5k=8,k=1.6,
∴y=1.6x;当 x＞5 时,设 y=k1x+b,由题意得{5k1+b=8,10k1+b=20,解得{k1=2.4,b=-4,
∴y=2.4x-4.综合以上得 y={1.6x,(0≤x≤5)2.4x-4.(x＞5)
(3)
∵76/5=15.2(元)＞8 元,
∴将 y=15.2 代入 y=2.4x-4 得 x=8,即人均用水为 8 吨,8×5=40(吨).答:该家庭这个月用了 40 吨生活用水.