《2025年课堂点睛八年级数学上册北师大版》

6. 如图,将长为8cm的橡皮筋放置在水平面上,固定两端A和B,然后把中点C垂直向上拉升3cm至点D,则橡皮筋被拉长了(A)

A.2cm
B.3cm
C.4cm
D.6cm

答案： A

7.(东营市中考)一艘船由A港沿北偏东$60^{\circ}$方向航行30km至B港,然后再沿北偏西$30^{\circ}$方向航行40km至C港,则A,C两港之间的距离为50km.

答案： 50

8. 公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾$a = 6$,弦$c = 10$,则小正方形ABCD的面积是4.

答案： 4

9.(易错题)如图,将一根长为24cm的筷子,置于底面直径为5cm、高为12cm的圆柱形水杯中,设筷子露出杯子外面的长为$h cm$,则h的取值范围是11≤h≤12.

答案： 11≤h≤12

10.(教材第6页随堂练习第1题变式)一辆装满货物,宽为2.4米,高4米的卡车,欲通过如图的隧道,该隧道截面上半部分为一个半圆形,则卡车能否顺利通过？

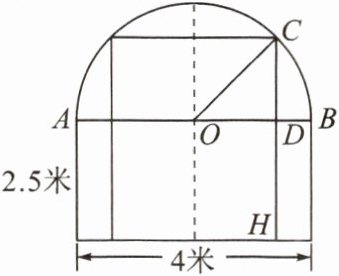
答案： 解:
∵车宽 2.4 米,
∴欲通过如图的隧道,只要比较距隧道中线 1.2米处的高度与车高.在 Rt△OCD中,由勾股定理可得 CD²=OC²-OD²=2²-1.2²=2.56,
∴CD=1.6 米,
∴CH=CD+DH=1.6+2.5=4.1(米).
∵4.1 米＞4 米,
∴卡车能顺利通过.

11.(教材第8页第5题改编)如图,在长方形ACDF中,$AC = DF$,点B在CD上,点E在DF上.$BC = DE = a$,$AC = BD = b$,$AB = BE = c$,且$AB\perp BE$.
(1)在探究长方形ACDF的面积S时,我们可以用两种不同的方法：一种是找到长和宽,然后利用长方形的面积公式,就可得到S；另一种是将长方形ACDF看成是由$\triangle ABC$,$\triangle BDE$,$\triangle AEF$,$\triangle ABE$组成的,分别求出它们的面积,再相加也可以得到S.请根据以上材料填空：
方法一：$S=$ab+b²；
方法二：$S = S_{\triangle ABC}+S_{\triangle BDE}+S_{\triangle AEF}+S_{\triangle ABE}=$ab+$\frac{1}{2}$b²-$\frac{1}{2}$a²+$\frac{1}{2}$c²；
(2)由于(1)中的两种方法表示的都是长方形ACDF的面积,因此它们应该相等,请利用以上的结论求a,b,c之间的等量关系；
(3)请直接运用(2)中的结论,求当$c = 10$,$a = 6$时,S的值.

(2)解:由题意得 ab+b²=ab+$\frac{1}{2}$b²-$\frac{1}{2}$a²+$\frac{1}{2}$c²,
∴2ab+2b²=2ab+b²-a²+c²,
∴a²+b²=c².
(3)
∵a²+b²=c²,且 c=10,a=6,
∴6²+b²=10²,
∴b=8,
∴S=ab+b²=6×8+64=112.

答案：
(1)ab+b² ab+$\frac{1}{2}$b²-$\frac{1}{2}$a²+$\frac{1}{2}$c²
(2)解:由题意得 ab+b²=ab+$\frac{1}{2}$b²-$\frac{1}{2}$a²+$\frac{1}{2}$c²,
∴2ab+2b²=2ab+b²-a²+c²,
∴a²+b²=c².
(3)
∵a²+b²=c²,且 c=10,a=6,
∴6²+b²=10²,
∴b=8,
∴S=ab+b²=6×8+64=112.