第97页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 离差平方和是各个数据与它们
平均数
之差的平方和,即 $ S= (x_{1}-\overline{x})^{2}+(x_{2}-\overline{x})^{2}+…+(x_{n}-\overline{x})^{2} $。
答案:
平均数
2.
方差
是各个数据与平均数之差的平方的平均数,即 $ s^{2}= \frac{1}{n}[(x_{1}-\overline{x})^{2}+(x_{2}-\overline{x})^{2}+…+(x_{n}-\overline{x})^{2}] $。而标准差
则是方差的算术
平方根。
答案:
方差 标准差 算术
3. 一组数据的方差或标准差越
小
,这组数据就越稳定。
答案:
小
省射击队要从甲、乙两名射击运动员中挑选一人参加全国比赛,在最近的 4 次选拔赛中,甲的射击的成绩如下(单位:环):7,8,9,8。
求甲运动员这 4 次选拔赛成绩的方差。
求甲运动员这 4 次选拔赛成绩的方差。
答案:
解:首先计算甲运动员这4次成绩的平均数:
$\bar{x} = \frac{7 + 8 + 9 + 8}{4} = 8 (环)$
然后根据方差公式计算方差:
$s^{2} = \frac{1}{4}[(7 - 8)^{2} + (8 - 8)^{2} + (9 - 8)^{2} + (8 - 8)^{2}] = \frac{1}{4}[(-1)^{2} + 0^{2} + 1^{2} + 0^{2}] = \frac{1}{4}(1 + 0 + 1 + 0) = 0.5$
故甲运动员这4次选拔赛成绩的方差为0.5。
$\bar{x} = \frac{7 + 8 + 9 + 8}{4} = 8 (环)$
然后根据方差公式计算方差:
$s^{2} = \frac{1}{4}[(7 - 8)^{2} + (8 - 8)^{2} + (9 - 8)^{2} + (8 - 8)^{2}] = \frac{1}{4}[(-1)^{2} + 0^{2} + 1^{2} + 0^{2}] = \frac{1}{4}(1 + 0 + 1 + 0) = 0.5$
故甲运动员这4次选拔赛成绩的方差为0.5。
1. 已知一组数据的方差是 3,则这组数据的标准差是(
A.9
B.3
C.1.5
D.$\sqrt{3}$
D
)A.9
B.3
C.1.5
D.$\sqrt{3}$
答案:
D
2.(凉山州中考)在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,每个团参加表演的 8 位女演员身高的折线统计图如下。则甲、乙两团女演员身高的方差 $ s_{甲}^{2} $、$ s_{乙}^{2} $ 大小关系正确的是(
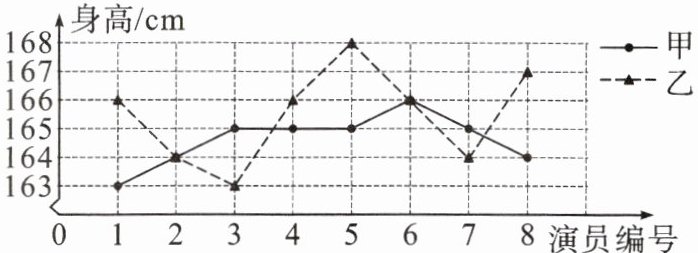
A.$ s_{甲}^{2} > s_{乙}^{2} $
B.$ s_{甲}^{2} < s_{乙}^{2} $
C.$ s_{甲}^{2} = s_{乙}^{2} $
D.无法确定
B
)
A.$ s_{甲}^{2} > s_{乙}^{2} $
B.$ s_{甲}^{2} < s_{乙}^{2} $
C.$ s_{甲}^{2} = s_{乙}^{2} $
D.无法确定
答案:
B
3.(衡阳市中考)某射击运动队进行了五次射击测试,甲、乙两名选手的测试成绩如下表。甲、乙两名选手成绩的方差分别记为 $ s_{甲}^{2} $ 和 $ s_{乙}^{2} $,则 $ s_{甲}^{2} $ 和 $ s_{乙}^{2} $ 的大小关系是(

A.$ s_{甲}^{2} > s_{乙}^{2} $
B.$ s_{甲}^{2} < s_{乙}^{2} $
C.$ s_{甲}^{2} = s_{乙}^{2} $
D.无法确定
A
)
A.$ s_{甲}^{2} > s_{乙}^{2} $
B.$ s_{甲}^{2} < s_{乙}^{2} $
C.$ s_{甲}^{2} = s_{乙}^{2} $
D.无法确定
答案:
A
4.(滨州市中考)某芭蕾舞团新进一批女演员,她们的身高及其对应人数情况如表所示:

那么,这批女演员身高的方差为

那么,这批女演员身高的方差为
2
。
答案:
2
5. 南京长江大桥连续七天的车流量(每日过桥车辆次数)分别为(单位:千辆/日):8.0,8.3,9.1,8.5,8.2,8.4,9.0,请计算这七天中车流量的方差和标准差。(方差、标准差精确到 0.01)
答案:
解:平均数为 $\overline{x}=\frac{1}{7}×(8.0+8.3+9.1+8.5+8.2+8.4+9.0)=8.5$(千辆/日),方差 $s^{2}=\frac{1}{7}×[(8.0-8.5)^{2}+(8.3-8.5)^{2}+\cdots +(9.0-8.5)^{2}]\approx 0.14$;标准差 $s=\sqrt{s^{2}}\approx0.38.$
查看更多完整答案,请扫码查看


