《2025年课堂点睛八年级数学上册北师大版》

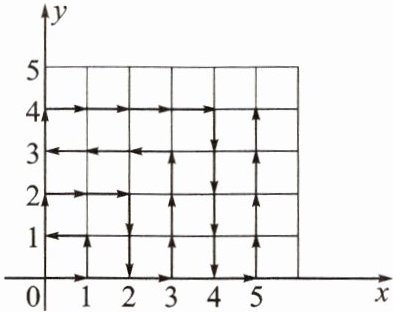
7. 如图,动点P从坐标原点(0,0)出发,以每秒一个单位长度的速度按图中箭头所示方向运动,第1秒运动到点(1,0),第2秒运动到点(1,1),第3秒运动到点(0,1),第4秒运动到点(0,2),…,则第2068秒点P所在位置的坐标是(45,43).

答案： (45,43)

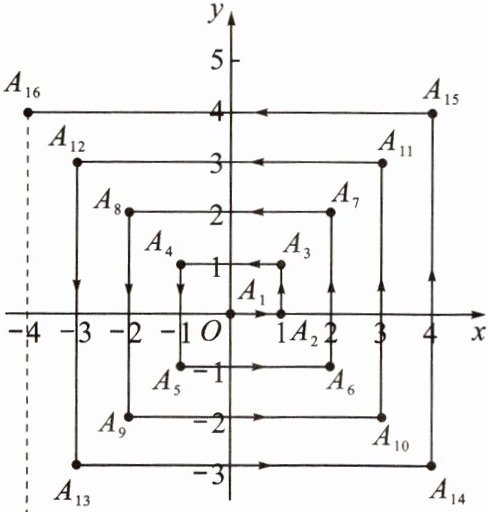
8. (潍坊市中考)在直角坐标系中,点$A_1$从原点出发,沿如图所示的方向运动,到达位置的坐标依次为$:A_2(1,0),A_3(1,1),A_4(-1,1),A_5(-1,-1),A_6(2,-1),A_7(2,2),….$若到达终点A_n(506,-505),则n的值为2022.

答案： 2022

9. 如图所示,正方形A_1A_2A_3A_4,A_5A_6A_7A_8,…(每个正方形的顶点从第一象限开始,按逆时针方向,依次记为A_1,A_2,A_3,A_4;A_5,A_6,A_7,A_8;…)的顶点都在格点上,各边均与x轴或y轴平行,它们的边长依次为2,4,…,则顶点$A_{30}$的坐标是____(-8,8).zyjl.cn/pic18/2025-09-17/49c2e9a5923db064aa5c7270a3e9c467.jpg?x-oss-process=image/crop,x_313,y_2230,w_430,h_413">

答案： (-8,8)

10. 如图,在平面直角坐标系xOy中,横、纵坐标都为整数的点称为整点.观察图中每一个正方形(实线)四条边上的整点的个数.
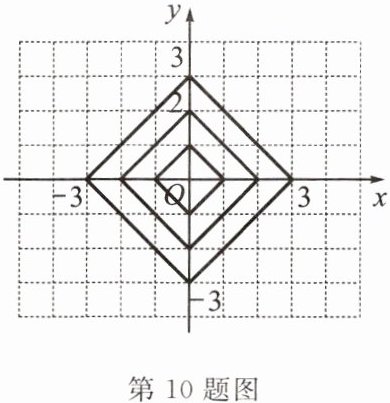
(1)画出由里向外的第4个正方形,则在第四个正方形上共有16个整点;
(2)请你猜测由里向外第10个正方形(实线)四条边上的整点共有40个;
(3)探究点P(-4,4)在第4个正方形的边上,(-2n,2n)在第2n个正方形的边上(n为正整数).

答案： 1. （1）
第$1$个正方形：
设正方形顶点坐标为$(\pm1,\pm1)$，四条边上的整点个数为$4×1 = 4$个（$(1,1),(1, - 1),(-1,1),(-1, - 1)$）。
第$2$个正方形：
顶点坐标为$(\pm2,\pm2)$，四条边上的整点个数为$4×2 = 8$个（$(2,2),(2, - 2),(-2,2),(-2, - 2)$以及$(2,0),(0,2),(-2,0),(0, - 2)$）。
第$3$个正方形：
顶点坐标为$(\pm3,\pm3)$，四条边上的整点个数为$4×3 = 12$个。
第$4$个正方形：
顶点坐标为$(\pm4,\pm4)$，四条边上的整点个数为$4×4 = 16$个。
2. （2）
由（1）可猜测第$n$个正方形四条边上的整点个数为$4n$个。
当$n = 10$时，$4n=4×10 = 40$个。
3. （3）
对于点$P(-4,4)$：
设点$P(x,y)$在第$m$个正方形上，根据规律$\vert x\vert+\vert y\vert=m + m$（因为正方形顶点坐标$(\pm m,\pm m)$，对于边上的点$(x,y)$满足$\vert x\vert+\vert y\vert = 2m$）。
已知$x=-4,y = 4$，则$\vert - 4\vert+\vert4\vert=8$，$2m = 8$，解得$m = 4$。
对于点$(-2n,2n)$：
同样根据$\vert x\vert+\vert y\vert=2m$，这里$x=-2n,y = 2n$，$\vert - 2n\vert+\vert2n\vert=4n$，又因为$4n = 2m$，所以$m = 2n$。
故答案依次为：（1）$16$；（2）$40$；（3）$4$；$2n$。

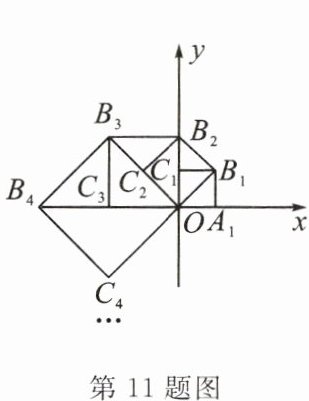
$11. $如图$,$在平面直角坐标系中$,$边长为$2$的正方形$OA_1B_1C_1$的两边在坐标轴上$,$以它的对角线$OB_1$为边作正方形$OB_1B_2C_2,$再以正方形$OB_1B_2C_2$的对角线$OB_2$为边作正方形$OB_2B_3C_3,…,$以此类推$,$则正方形$OB_{2023}B_{2024}C_{2024}$的顶点$B_{2024}$的坐标是$(2^{2013},0)$.　　

答案： $(2^{2013},0)$

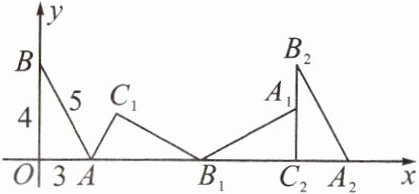
12. 如图,在平面直角坐标系中,将边长为3,4,5的Rt△ABO沿x轴向右滚动到△AB_1C_1的位置,再到△A_1B_1C_2的位置,…,依次进行下去,发现A(3,0),A_1(12,3),A_2(15,0),…,那么点$A_{2024}$的坐标为(12147,0).

答案： (12147,0)