第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
8. 计算$6÷\sqrt{3}×\frac{1}{\sqrt{3}}$所得的结果是
2
.
答案:
2
9. (河北省中考)若$a= \sqrt{2}$,$b= \sqrt{7}$,则$\sqrt{\frac{14a^2}{b^2}}= $(
A.2
B.4
C.$\sqrt{7}$
D.$\sqrt{2}$
A
)A.2
B.4
C.$\sqrt{7}$
D.$\sqrt{2}$
答案:
A
10. (荆州市中考)若$3-\sqrt{2}$的整数部分为$a$,小数部分为$b$,则代数式$(2+\sqrt{2}a)\cdot b$的值是
2
.
答案:
2
11. (创新题)如图,在长方形$ABCD中无重叠地放入面积分别为16cm^2和12cm^2$的两张正方形纸片,则图中空白部分的面积为
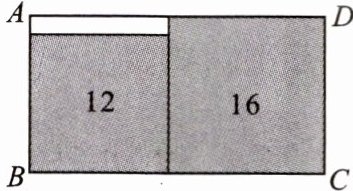
(-12+4√12)
$cm^2$.
答案:
(-12+4√12)
12. ;计算下列各式的值.
(1)$\frac{\sqrt{72}-\sqrt{16}}{\sqrt{8}}$;
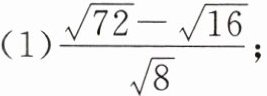
(2)$(\sqrt{\frac{8}{27}}-5\sqrt{6})×\sqrt{6}$;
(3)$(\sqrt{2}-1)^2-(\sqrt{2})^2$.
(1)$\frac{\sqrt{72}-\sqrt{16}}{\sqrt{8}}$;
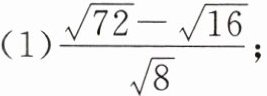
(2)$(\sqrt{\frac{8}{27}}-5\sqrt{6})×\sqrt{6}$;
(3)$(\sqrt{2}-1)^2-(\sqrt{2})^2$.
答案:
(1)解:原式=√72/√8-√16/√8=√9-√2=3-√2.
(2)解:原式=√(48/27)-5×6=4/3-30=-28 2/3.
(3)解:原式=2-2√2+1-2=1-2√2.
(1)解:原式=√72/√8-√16/√8=√9-√2=3-√2.
(2)解:原式=√(48/27)-5×6=4/3-30=-28 2/3.
(3)解:原式=2-2√2+1-2=1-2√2.
13. 如图,在$\triangle ABC$中,$\angle ACB= 90^{\circ}$,$AB= \sqrt{8}$,$BC= \sqrt{2}$,求斜边$AB上的高CD$的长.
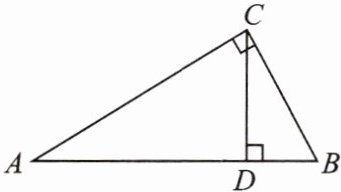

答案:
解:在Rt△ABC中,由勾股定理得AC=√(AB²-BC²)=√(8-2)=√6.因为S△ABC=1/2AC·BC=1/2CD·AB,所以CD=(AC·BC)/AB=(√6×√2)/√8=√(3/2).
14. (核心素养·创新意识)若$a+b= 2$,则称$a与b是关于1$的平衡数.
(1)$3$与
(2)若$(m+\sqrt{3})×(1-\sqrt{3})= -5+3\sqrt{3}$,判断$m+\sqrt{3}与5-\sqrt{3}是否是关于1$的平衡数,并说明理由.
(1)$3$与
-1
是关于$1$的平衡数,$5-\sqrt{2}$与______-3+√2
是关于$1$的平衡数;(2)若$(m+\sqrt{3})×(1-\sqrt{3})= -5+3\sqrt{3}$,判断$m+\sqrt{3}与5-\sqrt{3}是否是关于1$的平衡数,并说明理由.
答案:
(1)-1 -3+√2
(2)解:不是,理由如下:
∵(m+√3)×(1-√3)=m-√3m+√3-3,又
∵(m+√3)×(1-√3)=-5+3√3,
∴m-√3m+√3-3=-5+3√3,
∴m-√3m=-2+2√3.即m(1-√3)=-2(1-√3).
∴m=-2.
∴(m+√3)+(5-√3)=(-2+√3)+(5-√3)=3≠2,
∴(m+√3)与(5-√3)不是关于1的平衡数.
(1)-1 -3+√2
(2)解:不是,理由如下:
∵(m+√3)×(1-√3)=m-√3m+√3-3,又
∵(m+√3)×(1-√3)=-5+3√3,
∴m-√3m+√3-3=-5+3√3,
∴m-√3m=-2+2√3.即m(1-√3)=-2(1-√3).
∴m=-2.
∴(m+√3)+(5-√3)=(-2+√3)+(5-√3)=3≠2,
∴(m+√3)与(5-√3)不是关于1的平衡数.
查看更多完整答案,请扫码查看


