《2025年课堂点睛八年级数学上册北师大版》

7. 已知直角三角形中两边长分别为 6 和 8,则第三边的平方为100或28.

答案： 100或28

【变式】直角三角形的两条边分别为 3,4,则它的斜边为4或5.

答案： 4或5

8. 如图,在四边形$ABCD$中,$\angle DAB = \angle BCD = 90^{\circ}$,分别以四边形的四条边为边向外作四个正方形,若$S_{1}+S_{4}= 125$,$S_{3}= 46$,则$S_{2}$等于(B)

A.171
B.79
C.100
D.81
]

答案： B

9. 如图是由两个直角三角形和三个正方形组成的图形,大直角三角形的斜边和其中一直角边长分别是 13,12,则图中阴影部分的面积是(B)

A.16
B.25
C.144
D.169
]

答案： B

10. 在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,若$a = 6$,$b = 8$,则斜边$c = $10,斜边$c上的高h = $$\frac{24}{5}$.

答案： 10 $\frac{24}{5}$

11. 如图,图中的长方形的面积为51$cm^{2}$.
]

答案： 51

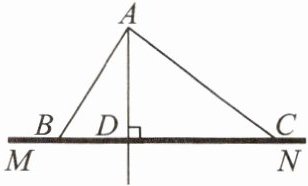
12. 如图,某斜拉桥的主梁$AD垂直于桥面MN于点D$,主梁上有两根拉索$AB$,$AC$,主梁$AD$的高度为 12 米,固定点$B$,$C$之间的距离为 21 米,$AC$的长为 20 米,则拉索$AB$的长为13米.
]

答案： 13米

13. 如图,在钝角三角形$ABC$中,已知$AB = 15$,$BC = 13$,$AC边上的高BD = 12$,求$AC$的长.
]

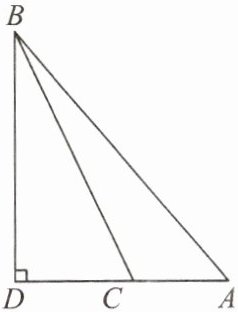
答案： 解:由题意得,在Rt△BCD中,BC=13,BD=12,
∴$CD^{2}=BC^{2}-BD^{2}=25$,
∴$CD=5$,在Rt△ABD中,AB=15,BD=12,
∴$AD^{2}=AB^{2}-BD^{2}=81$,
∴$AD=9$,
∴$AC=AD-CD=9-5=4$.

14.(核心素养·几何直观)(1)如图①所示,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$BC = a$,$AC = b$,$AB = c$,以$Rt\triangle ABC的三边长向外作的正方形的面积分别为S_{1}$,$S_{2}$,$S_{3}$,直接写出$S_{1}$,$S_{2}$,$S_{3}$之间存在的等量关系为$S_{1}+S_{2}=S_{3}$；
(2)如图②,如果以$Rt\triangle ABC$的三边长为直径向外作半圆,那么(1)中的结论是否成立？请说明理由；
(3)如图③,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,三边长分别为 5,12,13,分别以它的三边长为直径向上作半圆,求图③中阴影部分的面积.
]

答案：
(1)$S_{1}+S_{2}=S_{3}$
(2)解:成立,设直角三角形两条直角边BC,AC的长分别为a,b,斜边AB的长为c.
∴$S_{1}=\frac{1}{2}\pi\left(\frac{b}{2}\right)^{2}=\frac{b^{2}\pi}{8}$,$S_{2}=\frac{1}{2}\pi\left(\frac{a}{2}\right)^{2}=\frac{a^{2}\pi}{8}$,$S_{3}=\frac{1}{2}\pi\left(\frac{c}{2}\right)^{2}=\frac{c^{2}\pi}{8}$,由勾股定理,得$a^{2}+b^{2}=c^{2}$,
∴$\frac{a^{2}\pi}{8}+\frac{b^{2}\pi}{8}=\frac{\pi(a^{2}+b^{2})}{8}=\frac{\pi c^{2}}{8}$,
∴$S_{1}+S_{2}=S_{3}$.
(3)根据
(2)的结论,两个以直角边为直径的半圆面积和等于以斜边为直径的半圆面积.
∴$S_{阴影部分}=S_{直角三角形}$,
∴$S_{阴影部分}=\frac{1}{2}×5×12=30$.