第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
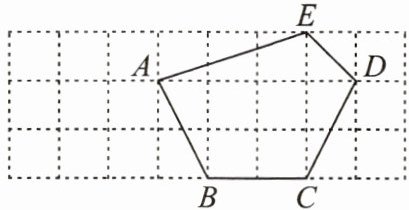
【变式4】如图,网格中每个小正方形的边长都是1,依次完成下列各问:
(1)任选一点作为原点,建立平面直角坐标系;
(2)写出A,B,C,D,E各点的坐标;
(3)求五边形ABCDE的面积.
(1)任选一点作为原点,建立平面直角坐标系;
(2)写出A,B,C,D,E各点的坐标;
(3)求五边形ABCDE的面积.

答案:
(1)解:如图所示
(2)A(0,2),B(1,0),C(3,0),D(4,2),E(3,3).
(3)S五边形ABCDE=S△ADE+S梯形ABCD=$\frac{1}{2}$×4×1+$\frac{(2 + 4)×2}{2}$=2 + 6=8.
(1)解:如图所示

(2)A(0,2),B(1,0),C(3,0),D(4,2),E(3,3).
(3)S五边形ABCDE=S△ADE+S梯形ABCD=$\frac{1}{2}$×4×1+$\frac{(2 + 4)×2}{2}$=2 + 6=8.
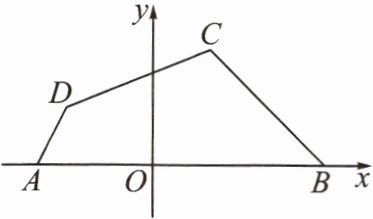
【拓展1】如图,A(-4,0),B(6,0),C(2,4),D(-3,2).
(1)求四边形ABCD的面积;
(2)求△BCD的面积;
(3)在y轴上找一点P,使△APB的面积等于四边形ABCD面积的一半.求P点的坐标.
(1)求四边形ABCD的面积;
(2)求△BCD的面积;
(3)在y轴上找一点P,使△APB的面积等于四边形ABCD面积的一半.求P点的坐标.

答案:
(1)解:作DE⊥x轴于点E,CF⊥x轴于点F.
∵A(-4,0),B(6,0),C(2,4),D(-3,2),
∴AE = 1,EF = 5,BF = 4,AB = 10,DE = 2,CF = 4,
∴S四边形ABCD=S△ADE+S四边形CDEF+S△BCF=$\frac{1}{2}$×1×2+$\frac{1}{2}$×(2 + 4)×5+$\frac{1}{2}$×4×4=24.
(2)S△BCD=S四边形ABCD - S△ABD=24 - $\frac{1}{2}$×10×2=14.
(3)
∵S△APB=$\frac{1}{2}$AB·OP=$\frac{1}{2}$×24,
∴OP = 2.4,
∴P点坐标为(0,2.4)或(0,-2.4).
(1)解:作DE⊥x轴于点E,CF⊥x轴于点F.
∵A(-4,0),B(6,0),C(2,4),D(-3,2),
∴AE = 1,EF = 5,BF = 4,AB = 10,DE = 2,CF = 4,
∴S四边形ABCD=S△ADE+S四边形CDEF+S△BCF=$\frac{1}{2}$×1×2+$\frac{1}{2}$×(2 + 4)×5+$\frac{1}{2}$×4×4=24.
(2)S△BCD=S四边形ABCD - S△ABD=24 - $\frac{1}{2}$×10×2=14.
(3)
∵S△APB=$\frac{1}{2}$AB·OP=$\frac{1}{2}$×24,
∴OP = 2.4,
∴P点坐标为(0,2.4)或(0,-2.4).
【拓展2】在平面直角坐标系中,O为原点,点A(0,2),B(-2,0),C(4,0).
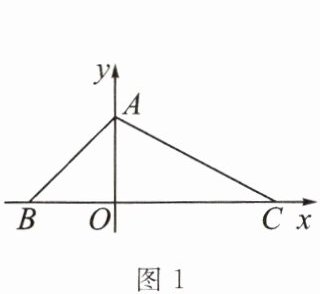
(1)如图1,三角形ABC的面积为
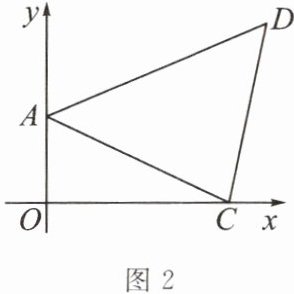
(2)如图2,将点B向右平移7个单位长度,再向上平移4个单位长度,得到对应点D.
①求三角形ACD的面积;
②P(m,3)是一动点,若三角形PAO的面积等于三角形AOC的面积,求出点P的坐标.
【方法指导】已知坐标系中图形的面积,求点的坐标时,可将点的横(纵)坐标转化为到坐标轴的距离,利用面积求得线段长,再转化为点的坐标.


(1)如图1,三角形ABC的面积为
6
;(2)如图2,将点B向右平移7个单位长度,再向上平移4个单位长度,得到对应点D.
①求三角形ACD的面积;
②P(m,3)是一动点,若三角形PAO的面积等于三角形AOC的面积,求出点P的坐标.
【方法指导】已知坐标系中图形的面积,求点的坐标时,可将点的横(纵)坐标转化为到坐标轴的距离,利用面积求得线段长,再转化为点的坐标.
(2)①连接OD.由题意,得D(5,4),S△ADC=S△AOD+S△ODC - S△AOC=$\frac{1}{2}$×2×5+$\frac{1}{2}$×4×4 - $\frac{1}{2}$×2×4=9.
②由题意,得$\frac{1}{2}$×2×|m|=$\frac{1}{2}$×2×4,解得m = ±4,
∴点P的坐标为(-4,3)或(4,3).
②由题意,得$\frac{1}{2}$×2×|m|=$\frac{1}{2}$×2×4,解得m = ±4,
∴点P的坐标为(-4,3)或(4,3).
答案:
(1)6 解:
∵点A(0,2),B(-2,0),C(4,0),
∴OA = 2,OB = 2,OC = 4,
∴S△ABC=$\frac{1}{2}$×(2 + 4)×2=6.
(2)①连接OD.由题意,得D(5,4),S△ADC=S△AOD+S△ODC - S△AOC=$\frac{1}{2}$×2×5+$\frac{1}{2}$×4×4 - $\frac{1}{2}$×2×4=9.
②由题意,得$\frac{1}{2}$×2×|m|=$\frac{1}{2}$×2×4,解得m = ±4,
∴点P的坐标为(-4,3)或(4,3).
(1)6 解:
∵点A(0,2),B(-2,0),C(4,0),
∴OA = 2,OB = 2,OC = 4,
∴S△ABC=$\frac{1}{2}$×(2 + 4)×2=6.
(2)①连接OD.由题意,得D(5,4),S△ADC=S△AOD+S△ODC - S△AOC=$\frac{1}{2}$×2×5+$\frac{1}{2}$×4×4 - $\frac{1}{2}$×2×4=9.
②由题意,得$\frac{1}{2}$×2×|m|=$\frac{1}{2}$×2×4,解得m = ±4,
∴点P的坐标为(-4,3)或(4,3).
查看更多完整答案,请扫码查看


