第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
直角三角形中,已知一边和另外两边的关系,一般应引入未知数,运用
勾股定理
建立方程求解。
答案:
勾股定理
《算法统宗》记载古人丈量田地的诗:“昨日丈量地回,记得长步整三十。广斜相并五十步,不知几亩及分厘。”其大意是:“昨天丈量了田地回到家,记得长方形的田地长为30步,宽和对角线之和为50步。不知该田的面积有多少?”请帮他算一算,该田的面积为多少平方步。
答案:
解:设该长方形田的宽为$x$步,则对角线长为$(50 - x)$步,由勾股定理,得$30^{2}+x^{2}= (50 - x)^{2}$,解得$x = 16$,
面积:$30×16 = 480$(平方步)。
答:该田的面积为480平方步。
面积:$30×16 = 480$(平方步)。
答:该田的面积为480平方步。
1. 如图所示,有一块直角三角形纸片$ABC$,$\angle ACB = 90^{\circ}$,$AC = 8cm$,$BC = 6cm$,将斜边$AB$翻折,使点$B落在直角边AC的延长线上的点E$处,折痕为$AD$,则$CE$的长为(
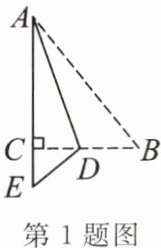
A.$1cm$
B.$2cm$
C.$3cm$
D.$4cm$
B
)
A.$1cm$
B.$2cm$
C.$3cm$
D.$4cm$
答案:
B
2. 如图,在$Rt\triangle ABC$中,$AB = 9$,$BC = 6$,$\angle B = 90^{\circ}$,将$\triangle ABC$折叠,使点$A与BC边的中点D$重合,折痕为$MN$,则线段$BN$的长为
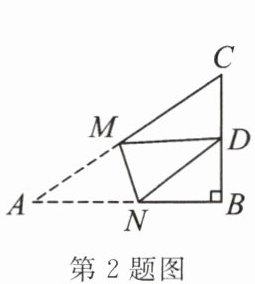
4
。
答案:
4
3. 如图所示,有一块直角三角形纸片$ABC$,量直角边$AC = 5cm$,$BC = 12cm$,现将直角边$AC沿直线AD$折叠,使点$C落在斜边AB$上,且与$AE$重合,求$CD$的长。
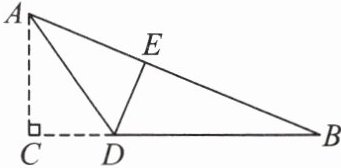

答案:
解:设CD=x,则DE=CD=x,AE=AC=5cm,∠AED=∠C=90°,在Rt△ABC中,AB²=AC²+BC²=5²+12²=169,
∴AB=13cm,
∴BE=AB - AE=13 - 5=8cm,BD=BC - CD=12 - x,在Rt△BED中,DE²+BE²=BD²,即x²+8²=(12 - x)²,解得x=$\frac{10}{3}$.
∴CD的长为$\frac{10}{3}$cm.
∴AB=13cm,
∴BE=AB - AE=13 - 5=8cm,BD=BC - CD=12 - x,在Rt△BED中,DE²+BE²=BD²,即x²+8²=(12 - x)²,解得x=$\frac{10}{3}$.
∴CD的长为$\frac{10}{3}$cm.
4. 如图,数学兴趣小组要测量学校旗杆的高度,同学们发现系在旗杆顶端的绳子垂到地面并多出一段(如图1),同学们首先测量了多出的这段绳子的长度为1米,再将绳子拉直(如图2),测出绳子末端$C到旗杆底部B$的距离为5米,则旗杆的高度为(

A.$5$米
B.$12$米
C.$13$米
D.$17$米
B
)
A.$5$米
B.$12$米
C.$13$米
D.$17$米
答案:
B
查看更多完整答案,请扫码查看


