第82页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
7.(原创题)如图是由同一种单位:cm长方形的墙砖粘贴的部分10墙面,其中3块横放的墙砖比1块竖放的墙砖高10cm,2块横放的墙砖比2块竖放的墙砖低40cm,则每块墙砖的面积是(
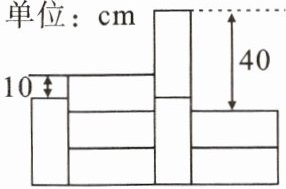
A.$425cm^2$
B.$525cm^2$
C.600cm^2$
D.$800cm^2$
B
)
A.$425cm^2$
B.$525cm^2$
C.600cm^2$
D.$800cm^2$
答案:
B
8.(教材第124页例3变式)已知一座桥长1000m,一列火车从桥上通过,测得火车从开始上桥到车身完全通过桥共用60s,而整列火车在桥上的时间是40s,则火车的长度为
200
m,火车的速度为20
m/s.
答案:
200 20
9.(教材第127页第13题变式)小明的爸爸骑着摩托车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下:
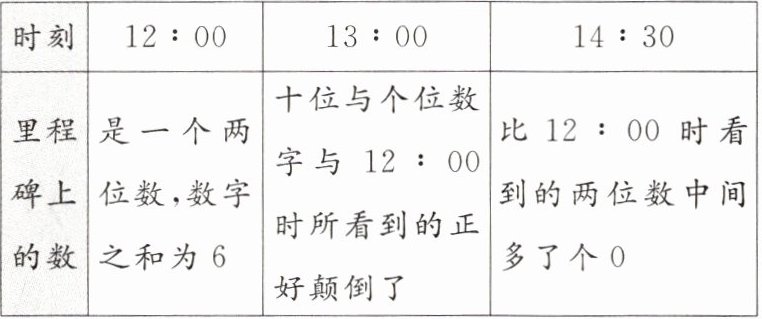
则12:00时看到的两位数是多少?

则12:00时看到的两位数是多少?
答案:
解:设 12:00 时看到的两位数个位是 y,十位为 x,即 10x+y,则 13:00和 14:30 时看到的两位数分别为 x+10y,100x+y,由题意可知,x+y=6 且 x<y,[(x+10y)-(10x+y)]×2.5=(100x+y)-(10x+y),这两个联立成方程组,解得{x=1,{y=5.10x+y=15.答:12:00 时看到的两位数是 15.
10.(核心素养·应用意识)滴滴快车是一种便捷的出行工具,计价规则如下表:
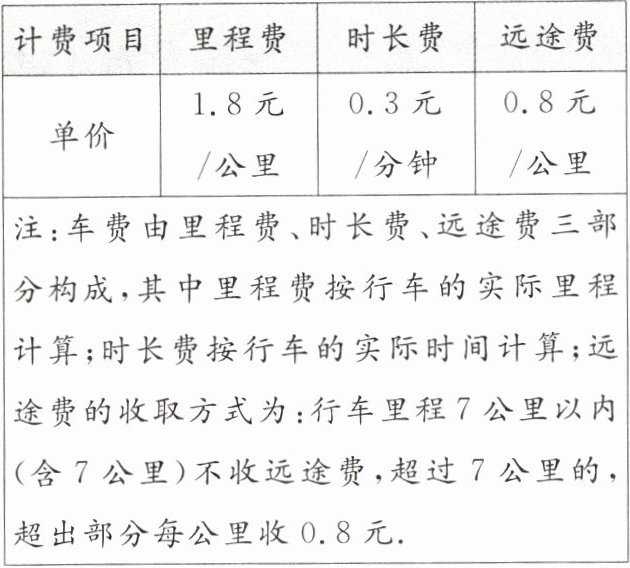
小王与小张各自乘坐滴滴快车,在同一地点约见,已知到达约见地点时他们的实际乘车里程分别为6公里与8.5公里,两人付给滴滴快车的乘车费相同.
(1)两人的实际乘车时间相差多少分钟?
(2)实际乘车时间较少的人,由于出发时间比另一人早,所以提前到达约见地点在大厅等候.已知他等候另一人的时间是他自己实际乘车时间的1.5倍,且比另一人的实际乘车时间的一半多8.5分钟,计算两人各自的实际乘车时间.

小王与小张各自乘坐滴滴快车,在同一地点约见,已知到达约见地点时他们的实际乘车里程分别为6公里与8.5公里,两人付给滴滴快车的乘车费相同.
(1)两人的实际乘车时间相差多少分钟?
(2)实际乘车时间较少的人,由于出发时间比另一人早,所以提前到达约见地点在大厅等候.已知他等候另一人的时间是他自己实际乘车时间的1.5倍,且比另一人的实际乘车时间的一半多8.5分钟,计算两人各自的实际乘车时间.
答案:
(1)设小王的实际乘车时间为$x$分钟,小张的实际乘车时间为$y$分钟。
根据计价规则,小王的乘车费用为:$1.8×6 + 0.3x$(因为$6\lt7$,无远途费)。
小张的乘车费用为:$1.8×8.5+0.3y + 0.8×(8.5 - 7)$。
因为两人乘车费相同,所以$1.8×6 + 0.3x=1.8×8.5+0.3y + 0.8×(8.5 - 7)$。
先计算等式右边:
$1.8×8.5+0.3y + 0.8×(8.5 - 7)=15.3+0.3y+0.8×1.5=15.3 + 0.3y+1.2=16.5+0.3y$。
等式左边为$10.8 + 0.3x$。
则$10.8 + 0.3x=16.5+0.3y$。
移项可得$0.3x-0.3y=16.5 - 10.8$。
根据乘法分配律$a(b - c)=ab - ac$,这里$0.3(x - y)=5.7$。
解得$x - y=\frac{5.7}{0.3}=19$。
所以两人的实际乘车时间相差$19$分钟。
(2)由(1)知$x=y + 19$,且$1.5y=\frac{1}{2}x+8.5$。
将$x=y + 19$代入$1.5y=\frac{1}{2}x+8.5$中:
$1.5y=\frac{1}{2}(y + 19)+8.5$。
去括号:根据$a(b + c)=ab+ac$,$\frac{1}{2}(y + 19)=\frac{1}{2}y+\frac{19}{2}$,则$1.5y=\frac{1}{2}y+\frac{19}{2}+8.5$。
因为$1.5=\frac{3}{2}$,$8.5=\frac{17}{2}$,所以$\frac{3}{2}y=\frac{1}{2}y+\frac{19 + 17}{2}$。
移项:$\frac{3}{2}y-\frac{1}{2}y=\frac{36}{2}$。
根据同分母分数减法$\frac{a}{c}-\frac{b}{c}=\frac{a - b}{c}(c\neq0)$,$\frac{3y - y}{2}=18$,即$\frac{2y}{2}=18$。
解得$y = 18$。
把$y = 18$代入$x=y + 19$,得$x=18 + 19=37$。
根据计价规则,小王的乘车费用为:$1.8×6 + 0.3x$(因为$6\lt7$,无远途费)。
小张的乘车费用为:$1.8×8.5+0.3y + 0.8×(8.5 - 7)$。
因为两人乘车费相同,所以$1.8×6 + 0.3x=1.8×8.5+0.3y + 0.8×(8.5 - 7)$。
先计算等式右边:
$1.8×8.5+0.3y + 0.8×(8.5 - 7)=15.3+0.3y+0.8×1.5=15.3 + 0.3y+1.2=16.5+0.3y$。
等式左边为$10.8 + 0.3x$。
则$10.8 + 0.3x=16.5+0.3y$。
移项可得$0.3x-0.3y=16.5 - 10.8$。
根据乘法分配律$a(b - c)=ab - ac$,这里$0.3(x - y)=5.7$。
解得$x - y=\frac{5.7}{0.3}=19$。
所以两人的实际乘车时间相差$19$分钟。
(2)由(1)知$x=y + 19$,且$1.5y=\frac{1}{2}x+8.5$。
将$x=y + 19$代入$1.5y=\frac{1}{2}x+8.5$中:
$1.5y=\frac{1}{2}(y + 19)+8.5$。
去括号:根据$a(b + c)=ab+ac$,$\frac{1}{2}(y + 19)=\frac{1}{2}y+\frac{19}{2}$,则$1.5y=\frac{1}{2}y+\frac{19}{2}+8.5$。
因为$1.5=\frac{3}{2}$,$8.5=\frac{17}{2}$,所以$\frac{3}{2}y=\frac{1}{2}y+\frac{19 + 17}{2}$。
移项:$\frac{3}{2}y-\frac{1}{2}y=\frac{36}{2}$。
根据同分母分数减法$\frac{a}{c}-\frac{b}{c}=\frac{a - b}{c}(c\neq0)$,$\frac{3y - y}{2}=18$,即$\frac{2y}{2}=18$。
解得$y = 18$。
把$y = 18$代入$x=y + 19$,得$x=18 + 19=37$。
查看更多完整答案,请扫码查看


