第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 甲、乙两人在一次百米赛跑中,路程$s$(米)与赛跑时间$t$(秒)的关系如图所示,则下列说法不正确的是(
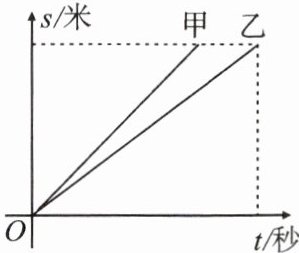
A.甲的速度大于乙的速度
B.甲先到达终点
C.甲、乙跑的路程相同
D.乙的成绩最好
D
)
A.甲的速度大于乙的速度
B.甲先到达终点
C.甲、乙跑的路程相同
D.乙的成绩最好
答案:
D
2. 在$20km$越野赛中,甲、乙两选手的行程$y(km)随时间x(h)$变化的图象如图,则下列说法中正确的是
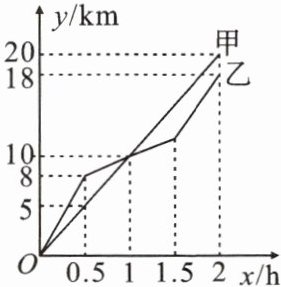
①两人相遇前,甲的速度小于乙的速度;
②出发后1小时,两人的行程均为$10km$;
③出发后$1.5$小时,甲的行程比乙多$3km$;
④甲比乙提前10分钟到达终点.
②③④
.(填序号)
①两人相遇前,甲的速度小于乙的速度;
②出发后1小时,两人的行程均为$10km$;
③出发后$1.5$小时,甲的行程比乙多$3km$;
④甲比乙提前10分钟到达终点.
答案:
②③④
3. 我市图书馆的租书业务有两种方式:会员卡和租书卡,分别使用这两种卡租书的租金$y$(元)与租书时间$x$(天)之间关系如图所示.当租书时间为50天时,采用
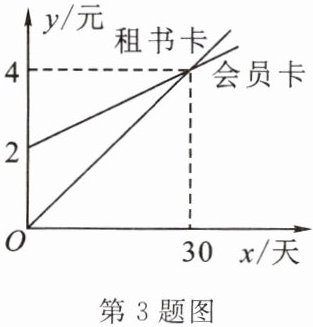
会员卡
租书方式比较省钱.
答案:
会员卡
4. 如图,$l_{1}$表示某产品一天的销售收入与销售量的关系;$l_{2}$表示该产品一天的销售成本与销售量的关系,则销售收入$y_{1}$(万元)与销售量$x$(万件)之间的函数关系式为
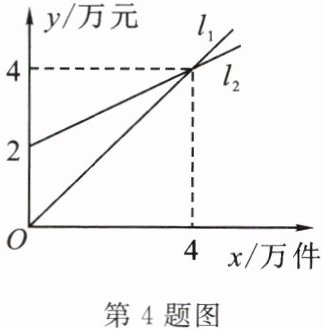
$y_{1}=x$
,销售成本$y_{2}$(万元)与销售量$x$(万件)之间的函数关系式为$y_{2}=\frac {1}{2}x+2$
.当一天的销售量$x$$>4$
时,销售该产品才能获利.
答案:
$y_{1}=x$ $y_{2}=\frac {1}{2}x+2$ $>4$
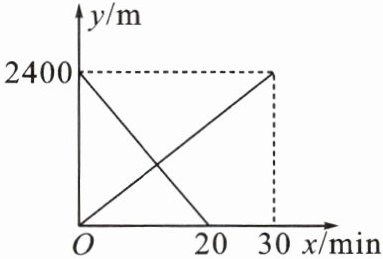
5. (盐城市中考)小丽从甲地匀速步行去乙地,小华骑自行车从乙地匀速前往甲地,同时出发.两人离甲地的距离$y(m)与出发时间x(min)$之间的函数关系如图所示.
(1)小丽步行的速度为______$m/min$;
(2)当两人相遇时,求他们到甲地的距离.
(1)
(2)
(1)小丽步行的速度为______$m/min$;
(2)当两人相遇时,求他们到甲地的距离.

(1)
80
(2)
解:由题意知,小丽离甲地的距离 y 与时间 x 的关系式为$y_{1}=80x$,设小华离甲地的距离 y 与时间 x 的关系式为$y_{2}=kx+b$,则$b=2400$,把$(20,0)$代入$y_{2}=kx+2400$,得$0=20k+2400$,解得$k=-120,\therefore y_{2}=-120x+2400$,当$y_{1}=y_{2}$时,即$80x=-120x+2400$,解得$x=12,\therefore$此时$y_{1}=y_{2}=80×12=960(m)$,即当两人相遇时,他们到甲地的距离是960m.
答案:
(1)80
(2)解:由题意知,小丽离甲地的距离 y 与时间 x 的关系式为$y_{1}=80x$,设小华离甲地的距离 y 与时间 x 的关系式为$y_{2}=kx+b$,则$b=2400$,把$(20,0)$代入$y_{2}=kx+2400$,得$0=20k+2400$,解得$k=-120,\therefore y_{2}=-120x+2400$,当$y_{1}=y_{2}$时,即$80x=-120x+2400$,解得$x=12,\therefore$此时$y_{1}=y_{2}=80×12=960(m)$,即当两人相遇时,他们到甲地的距离是960m.
(1)80
(2)解:由题意知,小丽离甲地的距离 y 与时间 x 的关系式为$y_{1}=80x$,设小华离甲地的距离 y 与时间 x 的关系式为$y_{2}=kx+b$,则$b=2400$,把$(20,0)$代入$y_{2}=kx+2400$,得$0=20k+2400$,解得$k=-120,\therefore y_{2}=-120x+2400$,当$y_{1}=y_{2}$时,即$80x=-120x+2400$,解得$x=12,\therefore$此时$y_{1}=y_{2}=80×12=960(m)$,即当两人相遇时,他们到甲地的距离是960m.
查看更多完整答案,请扫码查看


