《2025年课堂点睛八年级数学上册北师大版》

2. 勾股定理的简单应用：把实际问题转化为“直角三角形”模型,已知直角三角形的两边长,运用勾股定理可求第三边的长.

答案： 勾股定理

已知A,B两艘船同时从港口O出发,船A以20km/h的速度向东航行；船B以15km/h的速度向北航行.它们离开港口2h后,相距多远？

答案： 解：在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,
$\because S_{1} = 20$,$S_{2} = 11$,
$\therefore BC^{2} = AB^{2} - AC^{2} = 20 - 11 = 9$,
$\therefore BC = 3$。

1. 历史上对勾股定理的一种证法采用了如图图形,其中两个全等的直角三角形边AE,EB在一条直线上.证明中用到的面积相等的关系是(D)

A.$S_{\triangle EDA}= S_{\triangle CEB}$
B.$S_{\triangle EDA}+S_{\triangle CEB}= S_{\triangle CDE}$
C.$S_{四边形CDAE}= S_{四边形CDEB}$
D.$S_{\triangle EDA}+S_{\triangle CDE}+S_{\triangle CEB}= S_{四边形ABCD}$

答案： D

2. 如图,货车卸货时支架侧面是$Rt\triangle ABC$,其中$\angle ACB = 90^{\circ}$,已知$AB = 2.5m$,$AC = 2m$,则BC的长为(A)

A.1.5m
B.2m
C.2.5m
D.3m

答案： A

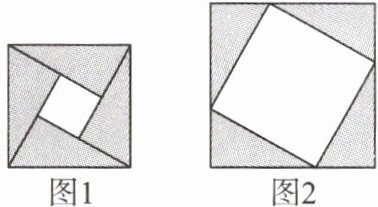
3.(眉山市中考改编)如图,图1是北京国际数学家大会的会标,它取材于我国古代数学家赵爽的“弦图”,是由四个全等的直角三角形拼成.若图1中大正方形的面积为24,小正方形的面积为4,现将这四个直角三角形拼成图2,则图2中大正方形的面积为44.

答案： 44

4. 如图,为修通铁路需凿通隧道AC,测得$\angle C = 90^{\circ}$,$AB = 5km$,$BC = 4km$,若每天开凿隧道0.3km,试计算需要几天才能把隧道AC凿通.

答案： 解:在 Rt△ABC 中,由勾股定理,得AC²=AB²-BC²=25-16=9,
∴AC=3km,3÷0.3=10(天).答:需要 10 天才能把隧道 AC 凿通.

5. 在$\triangle ABC$中,$AB = 13cm$,$AC = 20cm$,高$AD = 12cm$,则BC的长为11 或 21cm.
变式如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AB = 20$,$AC = 12$,若点P是射线BC上的一个动点,$AP = 15$,则BP的长为7 或 25.

答案： 11 或 21 【变式】7 或 25