《2025年课堂点睛八年级数学上册北师大版》

8. 观察下列几组勾股数,并填空:①6,8,10,②8,15,17,③10,24,26,④12,35,37,则第⑤组勾股数为14，48，50.

答案： 14，48，50

9. 如图为一个长方体纸盒,纸盒的长、宽、高分别是$6\mathrm{cm}$,$3\mathrm{cm}$,$2\mathrm{cm}$,则盒内可放木棒最长的长度是 (B)

A.$6\mathrm{cm}$
B.$7\mathrm{cm}$
C.$8\mathrm{cm}$
D.$9\mathrm{cm}$

答案： B

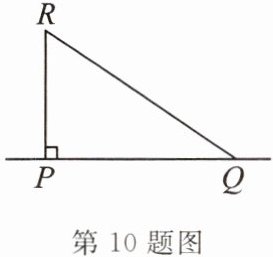
10. 一根 32 厘米的绳子被折成如图所示的形状,其两端钉在$P$,$Q$两点,$PQ = 16$厘米,且$RP\perp PQ$,则$RQ = $20厘米.

答案： 20

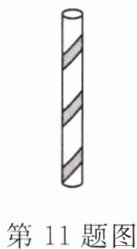
11. 如图是学校艺术馆中的柱子,高$4.5\mathrm{m}$. 为迎接艺术节的到来,工作人员用一条花带从柱底向柱顶均匀地缠绕 3 圈,一直缠到起点的正上方为止. 若柱子的底面周长是$2\mathrm{m}$,则这条花带至少需要7.5$\mathrm{m}$.

答案： 7.5

12. 如图,已知某学校$A与直线公路BD相距3000\mathrm{m}$,且与该公路上一个车站$D相距5000\mathrm{m}$,现要在公路边建一个超市$C$,使之与学校$A及车站D$的距离相等,那么该超市与车站$D$的距离是多少米?

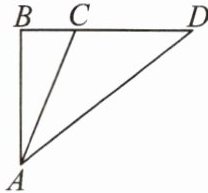
答案： 解：根据题意得 AC=CD，∠ABD=90°，在 Rt△ABD 中，AB=3000m，AD=5000m，
∴BD=4000m，设 CD=AC=xm，则 BC=(4000-x)m，在 Rt△ABC 中，AC²=AB²+BC²，即 x²=3000²+(4000-x)²，解得 x=3125．答：该超市与车站 D 的距离是 3125 米．

13. 若一直角三角形的两边长$a$,$b满足(a - 3)^{2}+|b - 4| = 0$,则该直角三角形的第三边长的平方为25 或 7.

答案： 25 或 7

14. 某等腰三角形的腰长为 5,一腰上的高为 3,则这个等腰三角形底边长的平方为10 或 90.

答案： 10 或 90

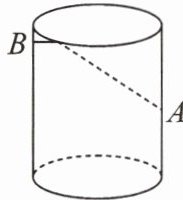
15. (广安市中考改编)如图,圆柱形玻璃杯的杯高为$9\mathrm{cm}$,底面周长为$16\mathrm{cm}$,在杯内壁离杯底$4\mathrm{cm}的点A$处有一滴蜂蜜,此时,一只蚂蚁正好在杯外壁上,它在离杯上沿$1\mathrm{cm}$,且与蜂蜜相对的点$B$处,则蚂蚁从外壁$B处到内壁A$处所走的最短路程为10$\mathrm{cm}$. (杯壁厚度不计)

答案： 10

16. 笔直的河流一侧有一旅游地$C$,河边有两个漂流点$A$,$B$. 其中$AB = AC$,由于某种原因,由$C到A$的路现在已经不通了,为方便游客,决定在河边新建一个漂流点$H(A$,$H$,$B$在同一直线上),并新修一条路$CH$,测得$BC = 5$千米,$CH = 4$千米,$BH = 3$千米.
(1) 判断$\triangle BCH$的形状,并说明理由；
(2) 求原路线$AC$的长.

答案： （1）解：△BCH 是直角三角形，理由：在△CHB 中，
∵CH²+BH²=4²+3²=25，BC²=25，
∴CH²+BH²=BC²，
∴△BCH 是直角三角形且∠CHB=90°． （2）设 AC=AB=x 千米，则 AH=AB-BH=(x-3)千米，在 Rt△ACH 中，由勾股定理得 AC²=AH²+CH²，
∴x²=(x-3)²+4²．解得 x=25/6．答：原路线 AC 的长为 25/6 千米．