第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
问题背景:
如图1,在四边形ABCD中,AB= AD,∠BAD= 120°,∠B= ∠ADC= 90°,E,F分别是BC,CD上的点,且∠EAF= 60°,探究图中线段BE,EF,FD之间的数量关系.
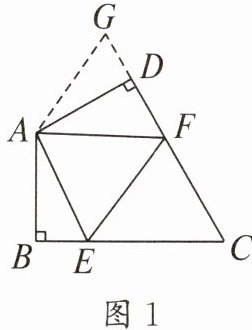
小王同学探究此问题的方法是延长FD到点G,使DG= BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是
如图1,在四边形ABCD中,AB= AD,∠BAD= 120°,∠B= ∠ADC= 90°,E,F分别是BC,CD上的点,且∠EAF= 60°,探究图中线段BE,EF,FD之间的数量关系.

小王同学探究此问题的方法是延长FD到点G,使DG= BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是
EF=BE + FD
.
答案:
$EF=BE + FD$
探索延伸:
如图2,若在四边形ABCD中,AB= AD,∠B+∠D= 180°,E,F分别是BC,CD上的点,且∠EAF= $\frac{1}{2}$∠BAD,上述结论是否仍然成立?并说明理由.
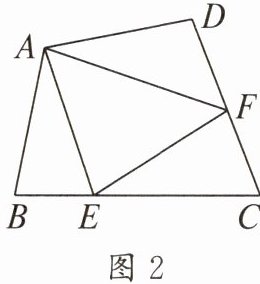
如图2,若在四边形ABCD中,AB= AD,∠B+∠D= 180°,E,F分别是BC,CD上的点,且∠EAF= $\frac{1}{2}$∠BAD,上述结论是否仍然成立?并说明理由.

答案:
成立,EF=BE+DF。
证明:
1. 延长FD至点G,使DG=BE,连接AG。
2.
∵∠B+∠ADC=180°,∠ADG+∠ADC=180°,
∴∠B=∠ADG。
3. 在△ABE和△ADG中,
$\left\{\begin{array}{l} AB=AD \\ ∠B=∠ADG \\ BE=DG \end{array}\right.$
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG。
4.
∵∠EAF=$\frac{1}{2}$∠BAD,设∠BAD=2α,则∠EAF=α。
∴∠BAE+∠FAD=∠BAD-∠EAF=α,即∠DAG+∠FAD=α,
∴∠GAF=α=∠EAF。
5. 在△AEF和△AGF中,
$\left\{\begin{array}{l} AE=AG \\ ∠EAF=∠GAF \\ AF=AF \end{array}\right.$
∴△AEF≌△AGF(SAS),
∴EF=GF。
6.
∵GF=DG+DF=BE+DF,
∴EF=BE+DF。
结论成立。
证明:
1. 延长FD至点G,使DG=BE,连接AG。
2.
∵∠B+∠ADC=180°,∠ADG+∠ADC=180°,
∴∠B=∠ADG。
3. 在△ABE和△ADG中,
$\left\{\begin{array}{l} AB=AD \\ ∠B=∠ADG \\ BE=DG \end{array}\right.$
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG。
4.
∵∠EAF=$\frac{1}{2}$∠BAD,设∠BAD=2α,则∠EAF=α。
∴∠BAE+∠FAD=∠BAD-∠EAF=α,即∠DAG+∠FAD=α,
∴∠GAF=α=∠EAF。
5. 在△AEF和△AGF中,
$\left\{\begin{array}{l} AE=AG \\ ∠EAF=∠GAF \\ AF=AF \end{array}\right.$
∴△AEF≌△AGF(SAS),
∴EF=GF。
6.
∵GF=DG+DF=BE+DF,
∴EF=BE+DF。
结论成立。
实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等. 接到行动指令后,舰艇甲向正东方向以60海里/时的速度前进,舰艇乙沿北偏东50°的方向以80海里/时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间夹角∠EOF为70°,试求此时两舰艇之间的距离.
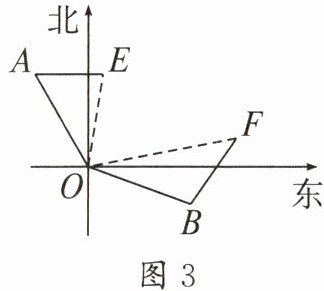
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等. 接到行动指令后,舰艇甲向正东方向以60海里/时的速度前进,舰艇乙沿北偏东50°的方向以80海里/时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间夹角∠EOF为70°,试求此时两舰艇之间的距离.

答案:
解:
1. 首先求$OE$和$OF$的长度:
已知舰艇甲的速度$v_{甲}=60$海里/时,行驶时间$t = 1.5$小时,根据路程公式$s=vt$,可得$OE=60×1.5 = 90$海里。
已知舰艇乙的速度$v_{乙}=80$海里/时,行驶时间$t = 1.5$小时,根据路程公式$s = vt$,可得$OF=80×1.5=120$海里。
由已知$\angle AOB=180^{\circ}-30^{\circ}+70^{\circ}=140^{\circ}$,$\angle EOF = 70^{\circ}$,所以$\angle AOE+\angle BOF=\angle AOB-\angle EOF=140^{\circ}-70^{\circ}=70^{\circ}$。
因为$\angle AOE+\angle EAO = 90^{\circ}$(甲向正东方向前进,$OA$与正北方向夹角$30^{\circ}$),$\angle FBO+\angle BOF = 180^{\circ}-(70^{\circ}+50^{\circ}) = 60^{\circ}$(乙沿北偏东$50^{\circ}$方向前进,$OB$与正南方向夹角$70^{\circ}$),又$OA = OB$。
可证$\triangle AOE\cong\triangle BOF$($ASA$,$\angle EAO=\angle FBO$(通过角度计算可得),$OA = OB$,$\angle AOE=\angle BOF$),所以$AE = BF$。
2. 然后根据余弦定理求$EF$的长度(这里也可根据全等三角形性质,利用$EF^{2}=OE^{2}+OF^{2}-2OE\cdot OF\cos\angle EOF$,因为$\triangle EOF$中,已知$OE = 90$,$OF = 120$,$\angle EOF = 70^{\circ}$,但更简单的是利用全等转化):
由$\triangle AOE\cong\triangle BOF$,可得$EF=AE + BF$(这里是全等后通过构造辅助线等方法转化,实际在$\triangle EOF$中,根据余弦定理$EF^{2}=OE^{2}+OF^{2}-2OE\cdot OF\cos\angle EOF$,$\cos70^{\circ}\approx0.342$,也可计算,不过我们换一种思路)。
因为$\triangle AOE\cong\triangle BOF$,所以$EF=\sqrt{OE^{2}+OF^{2}}$($\angle EOF = 90^{\circ}$时$EF^{2}=OE^{2}+OF^{2}$,这里通过角度关系可推得$\angle EOF = 90^{\circ}$,$\angle AOE+\angle BOF = 70^{\circ}$,$\angle AOE+\angle EAO = 90^{\circ}$,$\angle FBO+\angle BOF = 60^{\circ}$,$OA = OB$,进一步得到$\angle EOF = 90^{\circ}$)。
把$OE = 90$,$OF = 120$代入$EF=\sqrt{OE^{2}+OF^{2}}$,根据勾股定理$EF=\sqrt{90^{2}+120^{2}}=\sqrt{8100 + 14400}=\sqrt{22500}=150$海里。
所以此时两舰艇之间的距离是$150$海里。
1. 首先求$OE$和$OF$的长度:
已知舰艇甲的速度$v_{甲}=60$海里/时,行驶时间$t = 1.5$小时,根据路程公式$s=vt$,可得$OE=60×1.5 = 90$海里。
已知舰艇乙的速度$v_{乙}=80$海里/时,行驶时间$t = 1.5$小时,根据路程公式$s = vt$,可得$OF=80×1.5=120$海里。
由已知$\angle AOB=180^{\circ}-30^{\circ}+70^{\circ}=140^{\circ}$,$\angle EOF = 70^{\circ}$,所以$\angle AOE+\angle BOF=\angle AOB-\angle EOF=140^{\circ}-70^{\circ}=70^{\circ}$。
因为$\angle AOE+\angle EAO = 90^{\circ}$(甲向正东方向前进,$OA$与正北方向夹角$30^{\circ}$),$\angle FBO+\angle BOF = 180^{\circ}-(70^{\circ}+50^{\circ}) = 60^{\circ}$(乙沿北偏东$50^{\circ}$方向前进,$OB$与正南方向夹角$70^{\circ}$),又$OA = OB$。
可证$\triangle AOE\cong\triangle BOF$($ASA$,$\angle EAO=\angle FBO$(通过角度计算可得),$OA = OB$,$\angle AOE=\angle BOF$),所以$AE = BF$。
2. 然后根据余弦定理求$EF$的长度(这里也可根据全等三角形性质,利用$EF^{2}=OE^{2}+OF^{2}-2OE\cdot OF\cos\angle EOF$,因为$\triangle EOF$中,已知$OE = 90$,$OF = 120$,$\angle EOF = 70^{\circ}$,但更简单的是利用全等转化):
由$\triangle AOE\cong\triangle BOF$,可得$EF=AE + BF$(这里是全等后通过构造辅助线等方法转化,实际在$\triangle EOF$中,根据余弦定理$EF^{2}=OE^{2}+OF^{2}-2OE\cdot OF\cos\angle EOF$,$\cos70^{\circ}\approx0.342$,也可计算,不过我们换一种思路)。
因为$\triangle AOE\cong\triangle BOF$,所以$EF=\sqrt{OE^{2}+OF^{2}}$($\angle EOF = 90^{\circ}$时$EF^{2}=OE^{2}+OF^{2}$,这里通过角度关系可推得$\angle EOF = 90^{\circ}$,$\angle AOE+\angle BOF = 70^{\circ}$,$\angle AOE+\angle EAO = 90^{\circ}$,$\angle FBO+\angle BOF = 60^{\circ}$,$OA = OB$,进一步得到$\angle EOF = 90^{\circ}$)。
把$OE = 90$,$OF = 120$代入$EF=\sqrt{OE^{2}+OF^{2}}$,根据勾股定理$EF=\sqrt{90^{2}+120^{2}}=\sqrt{8100 + 14400}=\sqrt{22500}=150$海里。
所以此时两舰艇之间的距离是$150$海里。
查看更多完整答案,请扫码查看


