《2025年阳光课堂金牌练习册八年级数学上册人教版》

1. 如图,已知OA= OC,OB= OD,∠AOC= ∠BOD,求证△AOB≌△COD.

答案： 证明：
∵∠AOC=∠BOD，
∴∠AOC-∠AOD=∠BOD-∠AOD，即∠COD=∠AOB。
在△AOB和△COD中，
OA=OC（已知），
∠AOB=∠COD（已证），
OB=OD（已知），
∴△AOB≌△COD（SAS）。

【典型例题2】在新修的花园小区中,有一条“Z”字形绿色长廊AB—BC—CD. 如图,AB//CD,BE= CF,在AB,BC,CD三段绿色长廊上各修建一凉亭E,M,F,其中M是BC的中点,在凉亭M与F之间有一池塘,不能直接到达,连接ME,MF,要想知道M与F之间的距离,只需要测出线段ME的长度,这样做合适吗？请说明理由.

答案： 【解】这样做合适,理由如下：
因为AB//CD,所以∠B= ∠C.
因为点M是BC的中点,
所以MB= MC.
在△MEB与△MCF中,
$\left\{ \begin{array}{l} BE = CF, \\ \angle B = \angle C, \\ BM = CM, \end{array} \right. $
所以△MEB≌△MFC(SAS),
所以ME= MF.
故要想知道M与F之间的距离,只需要测出线段ME的长度即可.

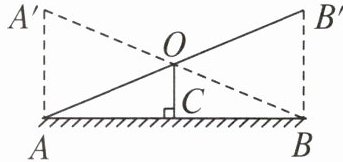
2. 小华和小宇玩跷跷板的示意图如图所示,横板绕它的中点O上下转动,立柱OC与地面垂直,当一方着地时,另一方上升到最高点. 在上下转动横板的过程中,两人上升的最大高度A'A,B'B有何数量关系？为什么？

答案： 解：$A^{\prime}A = B^{\prime}B$，理由如下：
因为$O$是$AB$、$A^{\prime}B^{\prime}$的中点，
所以$OA = OB^{\prime}$（中点的定义，线段中点将线段分为相等的两段），$OA^{\prime}=OB$。
在$\triangle AOA^{\prime}$与$\triangle BOB^{\prime}$中，
$\begin{cases}OA = OB^{\prime}\\\angle AOA^{\prime}=\angle BOB^{\prime}\ (对顶角相等)\\OA^{\prime}=OB\end{cases}$
根据$SAS$（边角边）判定定理，当两个三角形的两边及其夹角分别相等时，这两个三角形全等。
所以$\triangle AOA^{\prime}\cong\triangle BOB^{\prime}$。
所以$A^{\prime}A = B^{\prime}B$（全等三角形的对应边相等）。