《2025年阳光课堂金牌练习册八年级数学上册人教版》

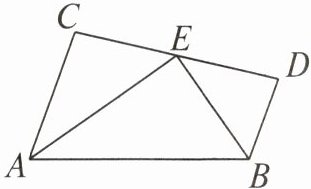
【典型例题1】如图,已知AC//BD,AE,BE分别平分∠CAB和∠DBA,CD过点E. 求证：AB= AC+BD.

答案：
思路导引 线段AC,BD与AB不在同一个三角形内,而且也不能直接找到联系三者的桥梁(如全等),因此可以考虑通过添加辅助线来构造联系三者的桥梁. 通过截长(补短)法求证三者之间的关系.
【证明】(方法1：截长法)如图,在线段AB上截取AF= AC,连接EF. 因为AE,BE分别平分∠CAB和∠DBA,所以∠1= ∠2,∠3= ∠4.

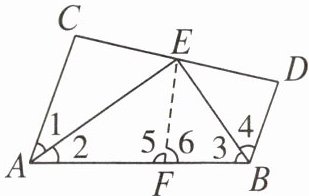
在△ACE和△AFE中,$\begin{cases}AC = AF,\\\angle1 = \angle2,\\AE = AE,\\\end{cases}\\ $
所以△ACE≌△AFE(SAS),
所以∠5= ∠C.
因为AC//BD,所以∠C+∠D= 180°.
又因为∠5+∠6= 180°,所以∠6= ∠D.
在△EFB和△EDB中,$\begin{cases}\angle6 = \angle D,\\\angle3 = \angle4,\\BE = BE,\\\end{cases}\\ $
所以△EFB≌△EDB(AAS),
所以BF= BD.
所以AB= AF+FB= AC+BD,
所以AB= AC+BD.
(方法二：补短法)如图,延长AC至点F,使AF= AB,连接EF.
因为AE,BE分别平分∠CAB和∠DBA,所以∠1= ∠2,∠3= ∠4.

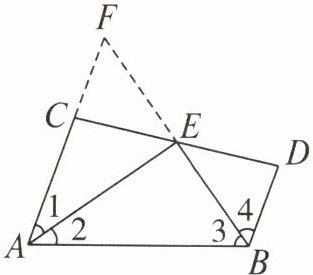
在△AEF和△AEB中,$\begin{cases}AF = AB,\\\angle1 = \angle2,\\AE = AE,\\\end{cases}\\ $
所以△AEF≌△AEB(SAS),
所以EF= EB,∠F= ∠3.
又因为∠3= ∠4,
所以∠F= ∠4.
因为AC//BD,
所以∠FCE= ∠D.
在△CEF和△DEB中,$\begin{cases}\angle FCE = \angle D,\\\angle F = \angle4,\\EF = EB,\\\end{cases}\\ $
所以△CEF≌△DEB(AAS),
所以FC= BD.
因为AB= AF= AC+FC,
所以AB= AC+BD.