第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. 如图,点B,F,C,E在同一直线上,AB= DE,∠B= ∠E,要运用“SAS”判定△ABC≌△DEF,还需补充一个条件,可以是(
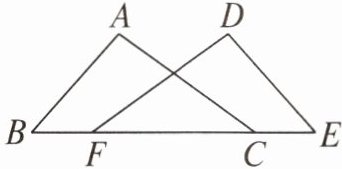
A.BF= EC
B.AC= FE
C.AC= DF
D.∠A= ∠D
A
)
A.BF= EC
B.AC= FE
C.AC= DF
D.∠A= ∠D
答案:
A
2. 如图,将两根钢条AA',BB'的中点O连在一起,使AA',BB'可以绕着点O自由转动,就做成了一个测量工具,则A'B'的长等于内槽宽AB,那么判定△OAB≌△OA'B'的基本事实简写为“
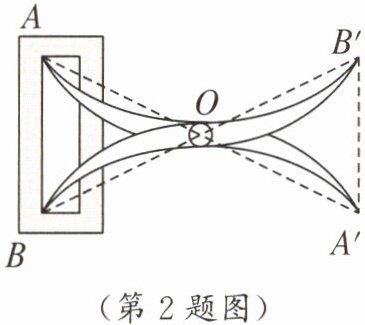
SAS
”.
答案:
$SAS$
3. 如图,一块三角形玻璃破裂成Ⅰ,Ⅱ两块,现需要配同样大小的一块三角形玻璃,为方便起见,只需带上第
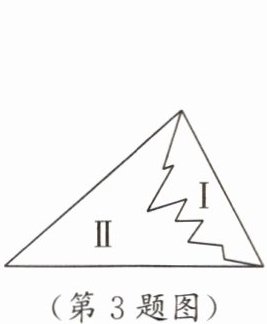
Ⅱ
块碎片.
答案:
Ⅱ
4. 在△ABC中,AB= 5,AC= 3,AD是△ABC的中线,设AD长为m,则m的取值范围是
1<m<4
.
答案:
$1\lt m\lt 4$(填写形式根据实际答题要求,这里若按区间形式对应选项填写)若题目是选项形式,根据常见情况假设本题是填空形式求范围,若转化为选择形式,答案选对应$1 < m<4$的选项。
5. 如图,在△ABC中,∠B= 50°,∠C= 20°. 过点A作AE⊥BC,垂足为E,延长EA至点D,使AD= AC. 在边AC上截取AF= AB,连接DF. 求证DF= CB.
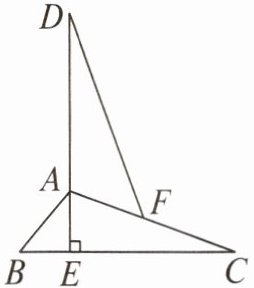

答案:
证明:
∵在△ABC中,∠B=50°,∠C=20°,
∴∠BAC=180°-∠B-∠C=180°-50°-20°=110°.
∵AE⊥BC,
∴∠AEC=90°.
在△AEC中,∠C=20°,∠AEC=90°,
∴∠EAC=180°-∠AEC-∠C=180°-90°-20°=70°.
∵D在EA的延长线上,
∴∠DAF=180°-∠EAC=180°-70°=110°,
∴∠DAF=∠BAC.
∵AD=AC,AF=AB,
∴△ADF≌△ACB(SAS),
∴DF=CB.
∵在△ABC中,∠B=50°,∠C=20°,
∴∠BAC=180°-∠B-∠C=180°-50°-20°=110°.
∵AE⊥BC,
∴∠AEC=90°.
在△AEC中,∠C=20°,∠AEC=90°,
∴∠EAC=180°-∠AEC-∠C=180°-90°-20°=70°.
∵D在EA的延长线上,
∴∠DAF=180°-∠EAC=180°-70°=110°,
∴∠DAF=∠BAC.
∵AD=AC,AF=AB,
∴△ADF≌△ACB(SAS),
∴DF=CB.
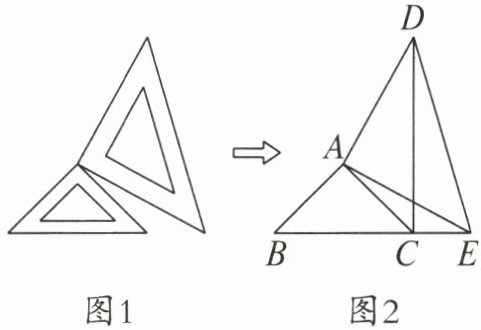
6. 两个大小不同的等腰直角三角尺如图1所示,图2是由它抽象出的几何图形,其中B,C,E在同一条直线上,连接DC.
(1)请找出图2中的全等三角形,并说明理由;
(2)求证DC⊥BE.
(1)请找出图2中的全等三角形,并说明理由;
(2)求证DC⊥BE.

答案:
(1) △ABE≌△ACD.
理由:
∵△ABC和△ADE是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°.
∴∠BAC+∠CAE=∠DAE+∠CAE,即∠BAE=∠CAD.
在△ABE和△ACD中,
$\left\{\begin{array}{l} AB=AC \\ ∠BAE=∠CAD \\ AE=AD \end{array}\right.$
∴△ABE≌△ACD(SAS).
(2) 证明:
∵△ABE≌△ACD,
∴∠ABE=∠ACD.
∵△ABC是等腰直角三角形,∠BAC=90°,
∴∠ABC=∠ACB=45°,即∠ABE=45°.
∴∠ACD=45°.
∵B,C,E在同一直线上,∠ACB=45°,
∴∠BCD=∠ACB+∠ACD=45°+45°=90°.
∴DC⊥BE.
(1) △ABE≌△ACD.
理由:
∵△ABC和△ADE是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°.
∴∠BAC+∠CAE=∠DAE+∠CAE,即∠BAE=∠CAD.
在△ABE和△ACD中,
$\left\{\begin{array}{l} AB=AC \\ ∠BAE=∠CAD \\ AE=AD \end{array}\right.$
∴△ABE≌△ACD(SAS).
(2) 证明:
∵△ABE≌△ACD,
∴∠ABE=∠ACD.
∵△ABC是等腰直角三角形,∠BAC=90°,
∴∠ABC=∠ACB=45°,即∠ABE=45°.
∴∠ACD=45°.
∵B,C,E在同一直线上,∠ACB=45°,
∴∠BCD=∠ACB+∠ACD=45°+45°=90°.
∴DC⊥BE.
查看更多完整答案,请扫码查看


