《2025年学习之友七年级数学上册人教版》

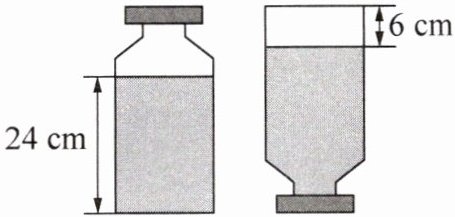
15. 如图,一个瓶子的容积为 $900 cm^{3}$,瓶内装着一些溶液.当瓶子正放时,瓶内溶液恰好为瓶子圆柱体部分,液体高度为24cm,当瓶子倒放时,空余部分圆柱体的高度为6cm.则瓶内溶液的体积为多少立方厘米？

答案： 解:设瓶子的底面积为S cm²,则24S+6S=900,解得S=30,瓶内溶液的体积为24×30=720(cm³),答:瓶内溶液的体积为720 cm³.

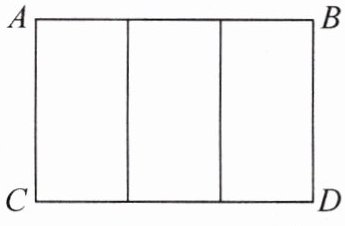
16. 如图是小颖用44根木棒拼成的一个横放的“目”字图形,已知 $AB:AC = 5:3$,每根木棒的长度为3cm,求这个图形的面积.

答案： 解:设AB由5x根木棒组成,则AC由3x根木棒组成,由题意得:2×5x+4×3x=44,解得x=2,经检验,符合题意,所以AB=5×2×3=30(cm),AC=3×2×3=18(cm),则30×18=540(cm²)答:这个图形的面积为540 cm².

1. 已知 $a + 1$ 与 $a - 3$ 互为相反数,则 $a = $1.

答案： 1

2. 已知 $\frac{x}{3} = \frac{y}{5} = k$,且 $x + y = 24$,则 $k$ 的值为3.

答案： 3

3. 若 $x = m$ 是关于 $x$ 的方程 $\frac{1}{2}x - m = 1$ 的解,则 $m$ 的值为(C)
A.0
B.2
C.$-2$
D.$-6$

答案： C

4. 若三个连续偶数的和为24,则它们的积为(B)
A.48
B.480
C.240
D.120

答案： B

5. 对任意四个有理数 $a$,$b$,$c$,$d$,定义新运算：$\begin{vmatrix}a&b\\c&d\end{vmatrix} = ad - bc$,已知 $\begin{vmatrix}2x&-4\\x&1\end{vmatrix} = 18$,则 $x$ 的值是3.

答案： 3

6. 如图,8块相同的长方形地砖拼成了一个长方形图案(地砖间的缝隙忽略不计),求每块地砖的宽.设每块地砖的宽为 $x cm$,根据题意,列出的方程为x+3x=60.

答案： x+3x=60