《2025年学习之友七年级数学上册人教版》

13. 如图,点A,点B,点C在数轴上表示的数为a,b,c,下列判断正确的是(D)

A.a＞b
B.b＞c
C.a＞c
D.c＞a

答案： D

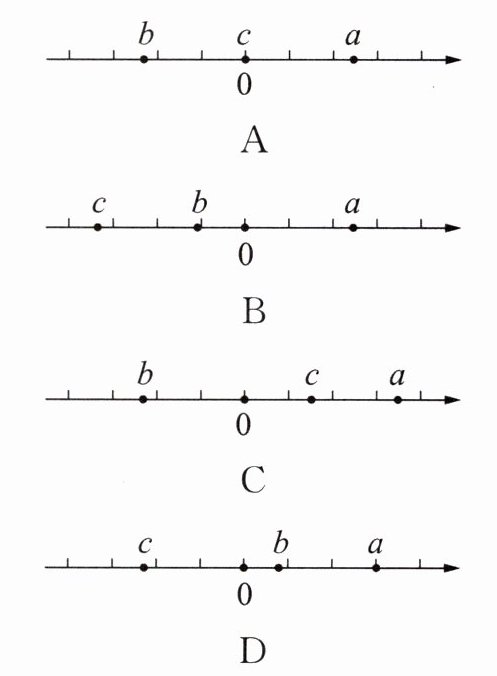
14. 已知三个数a,b,c中,a＞0,b＜0,c＜a,则这三个数在数轴上表示的位置不可能是(D)

答案： D

15. 比较下列各组数的大小：
(1)3与-7；
(2)-$\frac{5}{7}$和-$\frac{3}{4}$；
(3)|-8|与-8；
(4)-(-2.75)与-(-2.67)；
(5)-|-3.71|与-(-0.84).

答案：
(1)解:3 ＞ -7.
(2)解:$-\frac{5}{7} ＞ -\frac{3}{4}$.
(3)解:
∵|-8|=8
∴|-8| ＞ -8.
(4)解:
∵-(-2.75)=2.75,-(-2.67)=2.67而 2.75 ＞ 2.67
∴-(-2.75) ＞ -(-2.67).
(5)解:
∵-|-3.71|=-3.71-(-0.84)=0.84而 -3.71 ＜ 0.84
∴-|-3.71| ＜ -(-0.84).

1. 若|x|= 3,|y|= 2,且x＜y,求x和y.

答案： 解:
∵|x|=3,|y|=2,
∴x=±3,y=±2,而 x ＜ y
∴x=-3,y=±2

2. 如图,数轴上的三点A、B、C分别表示有理数a、b、c.

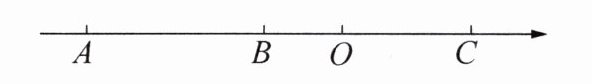
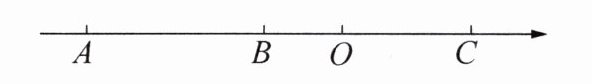
则：(1)a - b＜0,a + c____＜0,b - c____＜0.(用“＜”“＞”或“=”填空)
(2)你能把|a - b| - |a + c| + |b - c|化简吗？能的话,求出最后结果.

答案： 解:
(1)由数轴得，a-b ＜ 0,a+c ＜ 0,b-c ＜ 0,
(2)
∵a-b ＜ 0,a+c ＜ 0,b-c ＜ 0,
∴|a-b|-|a+c|+|b-c|=-(a-b)-[-(a+c)]+[-(b-c)]=-a+b+a+c-b+c=2c.

规定：符号min{a,b}表示a,b两个数中较小的一个,符号max{a,b}表示a,b两个数中较大的一个,例如：min{2,1}= 1,max{-1,2}= 2,请比较min{-0.$\dot{3}$,33%}与max{-$\frac{3}{4}$,-$\frac{2}{3}$}的大小.

答案： 解:根据“正数大于负数”可得,33% ＞ $-0.\dot{3}$所以 min{$-0.\dot{3}$,33%}=$-0.\dot{3}=-\frac{1}{3}$因为$-\frac{3}{4}=-\frac{9}{12},-\frac{2}{3}=-\frac{8}{12}$,且$\frac{9}{12} ＞ \frac{8}{12}$,根据“两个负数，绝对值大的反而小”可得$-\frac{9}{12} ＜ -\frac{8}{12}$,即$-\frac{3}{4} ＜ -\frac{2}{3}$,所以 max{$-\frac{3}{4},-\frac{2}{3}$}=$-\frac{2}{3}$,因为$\frac{1}{3} ＜ \frac{2}{3}$,所以$-\frac{1}{3} ＞ -\frac{2}{3}$,所以 min{$-0.\dot{3}$,33%} ＞ max{$-\frac{3}{4},-\frac{2}{3}$}.