《2025年点拨训练七年级数学上册沪科版安徽专版》

1. (12 分)如图,已知 $ OC $ 是 $ \angle AOB $ 内部的一条射线,$ OD $ 是 $ \angle AOB $ 的平分线,$ \angle AOC $ 与 $ \angle BOC $ 的度数比为 $ 3:2 $,且 $ \angle COD = 12^{\circ} $,求 $ \angle AOB $ 的度数。

解法一：(可以尝试用常规的算术法来解决!)
解法二：(可以尝试用方程来解决!)

答案： 解法一：因为∠AOC：∠BOC=3：2，所以∠AOC=$\frac{3}{2}$∠BOC.因为∠AOB=∠AOC+∠BOC，所以∠AOB=$\frac{5}{2}$∠BOC.因为 OD 平分∠AOB，所以∠AOD=$\frac{1}{2}$∠AOB=$\frac{5}{4}$∠BOC.所以∠COD=∠AOC-∠AOD=$\frac{3}{2}$∠BOC-$\frac{5}{4}$∠BOC=$\frac{1}{4}$∠BOC，即∠BOC=4∠COD. 因为∠COD=12°，所以∠BOC=48°，所以∠AOB=$\frac{5}{2}$∠BOC=120°.
解法二：因为∠AOC：∠BOC=3：2，所以可设∠AOC=(3x)°，∠BOC=(2x)°，所以∠AOB=∠AOC+∠BOC=(5x)°. 因为 OD 平分∠AOB，所以∠AOD=(2.5x)°. 因为∠COD=12°且∠COD=∠AOC-∠AOD，所以 3x-2.5x=12，解得 x=24，所以∠AOB=(5×24)°=120°.

2. (12 分)将一副三角板按如图所示摆放,$ \angle AOB = 60^{\circ} $,$ \angle COD = 45^{\circ} $,$ OM $ 平分 $ \angle AOD $,$ ON $ 平分 $ \angle COB $,求 $ \angle MON $ 的度数。

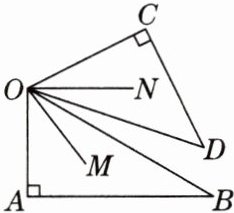
解法一：(可以尝试转化为角的和来计算!)
解法二：(可以尝试转化为角的差来计算!)

答案： 解法一：因为 OM 平分∠AOD，ON 平分∠COB，所以∠MOD=$\frac{1}{2}$∠AOD，∠NOB=$\frac{1}{2}$∠COB，所以∠MON=∠BOM+∠BOD+∠DON=∠MOD+∠NOB-∠BOD=$\frac{1}{2}$∠AOD+$\frac{1}{2}$∠COB-∠BOD=$\frac{1}{2}$（∠AOD+∠COB-2∠BOD）=$\frac{1}{2}$[（∠AOD-∠BOD）+（∠COB-∠BOD）]=$\frac{1}{2}$（∠AOB+∠COD）=$\frac{1}{2}$×（60°+45°）=52.5°.
解法二：因为 OM 平分∠AOD，ON 平分∠COB，所以∠AOM=$\frac{1}{2}$∠AOD，∠CON=$\frac{1}{2}$∠COB，所以∠MON=∠AOC-（∠AOM+∠CON）=（∠AOB+∠BOD+∠COD）-（$\frac{1}{2}$∠AOD+$\frac{1}{2}$∠BOC）=（∠AOB+∠BOD+∠COD）-$\frac{1}{2}$（∠AOB+∠BOD+∠COD+∠BOD）=（∠AOB+∠BOD+∠COD）-$\frac{1}{2}$（∠AOB+2∠BOD+∠COD）=∠AOB+∠BOD+∠COD-$\frac{1}{2}$∠AOB-∠BOD-$\frac{1}{2}$∠COD=$\frac{1}{2}$（∠AOB+∠COD）=$\frac{1}{2}$×（60°+45°）=52.5°.