第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
9. 小华在计算$14 - a$时,误把“$-$”看成“$+$”,求得结果为$-5$,则$14 - a= $
33
。
答案:
33
10. 创新题·新考法在如图所示的各个圆圈内填上适当的数,使每个圆圈里的数都等于与它相邻的两个数的和,则$m$的值为(
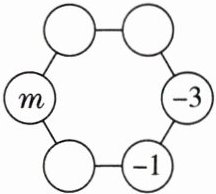
A.$3$
B.$2$
C.$-2$
D.$-5$
A
)
A.$3$
B.$2$
C.$-2$
D.$-5$
答案:
A
11. 分类讨论思想[2025·安庆月考]已知$\vert a\vert = 5$,$\vert b\vert = 3$,且$a + b\lt0$,则$a - b$的值为(
A.$-8$
B.$-2$
C.$-2或-8$
D.$2$
C
)A.$-8$
B.$-2$
C.$-2或-8$
D.$2$
答案:
C
12. [2025年1月合肥期末]如图,数轴上的点$A$、$B分别对应有理数a$、$b$,下列结论中正确的是(
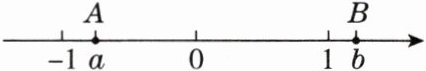
A.$a + b\lt0$
B.$-a + b\lt0$
C.$a - b\lt0$
D.$-a - b\gt0$
C
)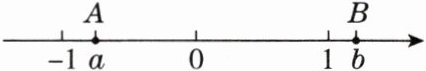
A.$a + b\lt0$
B.$-a + b\lt0$
C.$a - b\lt0$
D.$-a - b\gt0$
答案:
C
13. (12分)真实情境[2025年1月盐城期末]生活中,通常用24时计时法表示具体时间.与之相关,全球共分为24个时区,相邻两个时区的时间相差1小时,以英国格林威治所在的本初子午线为基准,在格林威治以东的地区,时差以“$+$”标记,在格林威治以西的地区,时差以“$-$”标记,下表是各城市与格林威治的时差:
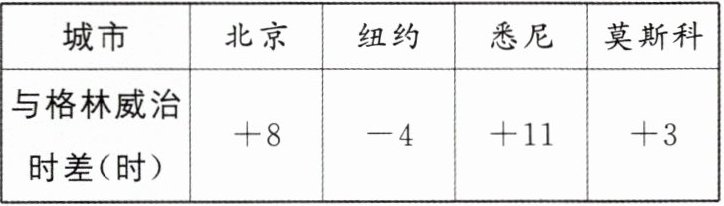
例如:格林威治12时,对应北京当地时间20时,对应纽约当地时间8时.
(1)莫斯科和纽约的时差是多少小时?
(2)若在悉尼的小明22时打电话给在纽约的小亮,则纽约当地时间是几时?
(3)小明将在11月14日21时乘坐北京直飞悉尼的飞机,经过12小时抵达,此时悉尼当地时间为11月几日的几时?

例如:格林威治12时,对应北京当地时间20时,对应纽约当地时间8时.
(1)莫斯科和纽约的时差是多少小时?
(2)若在悉尼的小明22时打电话给在纽约的小亮,则纽约当地时间是几时?
(3)小明将在11月14日21时乘坐北京直飞悉尼的飞机,经过12小时抵达,此时悉尼当地时间为11月几日的几时?
答案:
13.解:
(1)莫斯科和纽约的时差是7小时.
(2)纽约当地时间是7时.
(3)经过12小时抵达,此时悉尼当地时间为11月15日的12时.
(1)莫斯科和纽约的时差是7小时.
(2)纽约当地时间是7时.
(3)经过12小时抵达,此时悉尼当地时间为11月15日的12时.
14. (12分)几何直观阅读理解:数轴上线段的长度可以用线段端点表示的数进行减法运算得到.例:如图,线段$AB = 1 = 0 - (-1)$,线段$BC = 2 = 2 - 0$,线段$AC = 3 = 2 - (-1)$.
解决问题:
(1)数轴上点$M$、$N表示的数分别为-9和1$,则线段$MN= $
(2)数轴上点$E$、$F表示的数分别为-6和-3$,则线段$EF= $
(3)数轴上的两个点之间的距离为5,其中一个点表示的数为2,另一个点表示的数为$m$,求$m$。

解决问题:
(1)数轴上点$M$、$N表示的数分别为-9和1$,则线段$MN= $
10
;(2)数轴上点$E$、$F表示的数分别为-6和-3$,则线段$EF= $
3
;(3)数轴上的两个点之间的距离为5,其中一个点表示的数为2,另一个点表示的数为$m$,求$m$。
由题意,得$|m-2|=5$,解得$m=-3$或7,即m的值为-3或7.

答案:
14.解:
(1)10
(2)3
(3)由题意,得$|m-2|=5$,解得$m=-3$或7,即m的值为-3或7.
(1)10
(2)3
(3)由题意,得$|m-2|=5$,解得$m=-3$或7,即m的值为-3或7.
查看更多完整答案,请扫码查看


