《2025年点拨训练七年级数学上册沪科版安徽专版》

1. 通过观察归纳,给出下面每一列数中的后两项.
(1)4,6,8,10,12,14,16,18；
(2)0,3,8,15,24,35,48,63.

答案：
(1)16;18
(2)48;63

2. 已知一列数：1,$\frac{3}{4}$,$\frac{5}{9}$,$\frac{7}{16}$,$\frac{9}{25}$…用式子表示第 $n$ 个数,则第 $n$ 个数是$\frac{2n-1}{n^{2}}$.

答案： $\frac{2n-1}{n^{2}}$

3. 创新题·新题型如图为手的示意图,在各个手指间标记字母 $A$,$B$,$C$,$D$. 请按图中箭头所指方向(即 $A→B→C→D→C→B→A→B→C→…$ 的方式)从 $A$ 开始数连续的正整数 $1$,$2$,$3$,$4$,$5$,…$$,请你寻找规律,指出当字母 $B$ 第 $ 2025 $ 次出现时,恰好数到的数为(D)

A.$ 6064 $
B.$ 6066 $
C.$ 6060 $
D.$ 6074 $

答案： D

4. (12 分)[2024·盐城期中]【规律探索】请观察下面的点阵图和相应的等式,探究其中的规律：

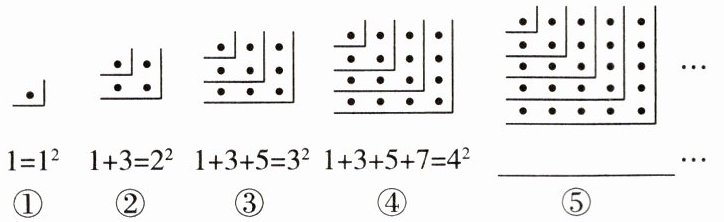
(1)在⑤的横线上写出相应的等式；1+3+5+7+9=5²
【规律归纳】
(2)试用含有 $n$ 的式子表示这一规律：$ 1 + 3 + 5 + 7 + 9 + … + $(2n-1)$=n^{2}$($n$ 为正整数)；
【规律应用】
(3)请用上述规律计算：$ 1 + 3 + 5 + … + 89 $.
1+3+5+…+89=45²=2025

答案：
(1)$1+3+5+7+9=5^{2}$
(2)$(2n-1)$
(3)$1+3+5+\cdots+89=45^{2}=2025$.

5. [2024·山西二模]数学美的表现形式是多种多样的,如图是由一些火柴搭成的“美”字的图案. 图①中用了 $9$ 根火柴,图②中用了 $17$ 根火柴,图③中用了 $25$ 根火柴,…$$,按照此规律,图ⓝ中用了$(8n+1)$根火柴(用含 $n$ 的代数式表示).

答案： $(8n+1)$

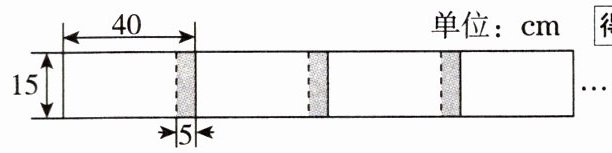
6. 将长为 $40$ cm、宽为 $15$ cm 的长方形白纸,按如图所示的方法黏合起来,黏合部分宽度为 $5$ cm,则 $n$ 张白纸黏合的总长度为$(35n+5)$cm.

答案： $(35n+5)$

7. 教材改编题一张长方形桌子可坐 $6$ 人,按图中方式将桌子拼在一起.

(1) $2$ 张桌子拼在一起可坐 $8$ 人,$4$ 张桌子拼在一起可坐12人,$n$ 张桌子拼在一起可坐$(4+2n)$人；
(2)一家餐厅有 $40$ 张这样的长方形桌子,按图中方式每 $5$ 张拼成 $1$ 张大桌子,则 $40$ 张桌子可拼成8张大桌子,共可坐112人.

答案：
(1)12;$(4+2n)$
(2)8;112