《2025年点拨训练七年级数学上册沪科版安徽专版》

11. 如图,数轴的单位长度为$1$,如果点$R$,$T$表示的数互为相反数,那么图中的$4$个点中,点P表示的数的绝对值最大。

答案： P

12. 易错题 若$\vert a\vert=1$,$\vert b\vert=2$,则在数轴上表示$a$,$b$的点之间的距离是3 或 1。

答案： 3 或 1

13. (8分)真实情境 [2025·合肥五十中月考]世乒赛中用球的质量有严格的规定,下表是$6$个乒乓球质量检测的结果(单位：克,超过标准质量的克数记为正数,不足标准质量的克数记为负数)。

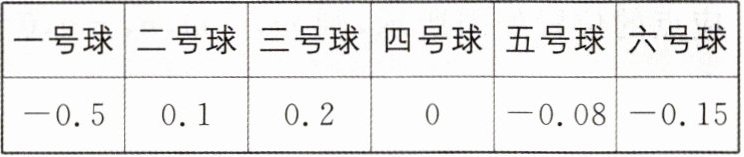
(1)请找出三个误差相对较小一些的乒乓球,并用绝对值的知识说明；
(2)若规定与标准质量误差不超过$0.1g$的为优等品,超过$0.1g但不超过0.3g$的为合格品,在这六个乒乓球中,优等品、合格品和不合格品分别是哪几个乒乓球？

答案：
(1)$|-0.5|=0.5$，$|0.1|=0.1$，$|0.2|=0.2$，$|0|=0$，$|-0.08|=0.08$，$|-0.15|=0.15$. 因为$0＜0.08＜0.1＜0.15＜0.2＜0.5$，所以三个误差相对较小一些的乒乓球为二号球、四号球和五号球；
(2)优等品是二号球、四号球、五号球；合格品是三号球、六号球；不合格品是一号球

14. (12分)中考趋势·阅读理解 [2025年1月淮北期末]阅读下列材料：
我们知道$\vert x\vert的几何意义是数轴上数x$的对应点与原点之间的距离,即$\vert x\vert=\vert x - 0\vert$,也可以说,$\vert x\vert表示数轴上数x与数0$对应点之间的距离。这个结论可以推广为$\vert A - B\vert表示数轴上数A与数B$对应点之间的距离。
(1)用绝对值表示数轴上$-5与3$对应点之间的距离；
(2)若$\vert x - 2\vert=3$,则$x$可以表示数轴上的哪些数？
(3)利用数轴找出所有符合条件的整数$x$,使得$\vert x - 3\vert+\vert x - (-4)\vert=7$成立,这样的整数是____。
(1)|-5-3|；
(2)-1或5；
(3)-4或-3或-2或-1或 0 或 1 或 2 或 3

答案：
(1)$|-5-3|$；
(2)$-1$或$5$；
(3)$-4$或$-3$或$-2$或$-1$或 0 或 1 或 2 或 3

1. 若$\vert a\vert+\vert b\vert=0$,则$a与b$的大小关系一定是(A)
A.$a = b = 0$
B.$a与b$不相等
C.$a与b$互为相反数
D.$a与b$异号

答案： A

2. 若$\vert m - 1\vert+\vert n - 3\vert=0$,则$m= $1,$n= $3。

答案： 1；3

3. (1)当$x= $2025时,$\vert x - 2025\vert$有最小值,这个最小值是0。
(2)当$x= $5时,$2025-\vert x - 5\vert$有最大值,这个最大值是2025。

答案：
(1)2025；0；
(2)5；2025