《2025年启东中学作业本八年级数学上册苏科版盐城专版》

1.(2024·南通期中)在下列四组数中,属于勾股数的是 (B)
A.0.3,0.4,0.5
B.9,40,41
C.2,3,4
D.1,$\sqrt{2}$,$\sqrt{3}$

答案： B

2.满足下列条件的$\triangle ABC$不是直角三角形的是 (D)
A.$BC= 1,AC= 2,AB= \sqrt{3}$
B.$BC:AC:AB= 3:4:5$
C.$\angle A+\angle B= \angle C$
D.$\angle A:\angle B:\angle C= 3:4:5$

答案： D

3.一个三角形的三边长分别为5,12,13,则这个三角形最长边上的中线长为6.5.

答案： 6.5

4.勾股数是指能成为直角三角形三条边长的三个正整数,世界上第一次给出勾股数公式的是中国古代数学著作《九章算术》.现有勾股数$a,b,c$,其中$a,b均小于c$,$a= \frac{1}{2}m^{2}-\frac{1}{2}$,$c= \frac{1}{2}m^{2}+\frac{1}{2}$,$m$是大于1的奇数,则$b= $m.(用含$m$的式子表示)

答案： m

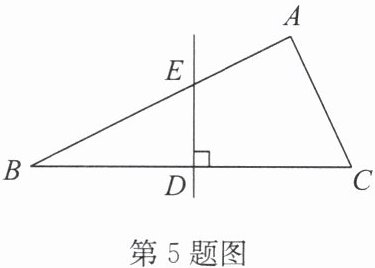
5.(2024·启东期中)如图,在$\triangle ABC$中,$AE= 3,BE= 5,AC= 4,DE是BC$的垂直平分线,交$BC于点D$,交$AB于点E$.求证:$\triangle ABC$为直角三角形.

答案：
证明:如答图，连接CE.
∵DE是BC的垂直平分线，
∴EC=BE=5.
　又
∵AE=3,AC=4,
∴AC²+AE²=4²+3²=25,EC²=5²=25,
∴AC²+AE²=EC²,
∴△AEC是直角三角形，且∠A=90°,
∴△ABC是直角三角形.
　　　　　　

6.勾股定理最早出现在《周髀算经》：“勾广三,股修四,弦隅五”.观察下列勾股数：3,4,5;5,12,13;7,24,25;…;这类勾股数的特点如下:勾为奇数,弦与股相差1,柏拉图研究了勾为偶数,弦与股相差2的一类勾股数,如6,8,10;8,15,17;…;若此类勾股数的勾为$2m(m\geq3,m$为正整数),则其弦是(结果用含$m$的式子表示) (C)
A.$m^{2}-1$
B.$2m+2$
C.$m^{2}+1$
D.$2m+3$

答案： C

7.《九章算术》是中国古代重要的数学著作,该著作中给出了勾股数$a,b,c$的计算公式:$a= \frac{1}{2}(m^{2}-n^{2})$,$b= mn$,$c= \frac{1}{2}(m^{2}+n^{2})$,其中$m＞n＞0$,$m,n$是互质的奇数.下列四组勾股数中,不能由该勾股数计算公式直接得出的是 (C)
A.3,4,5
B.5,12,13
C.6,8,10
D.7,24,25

答案： C