《2025年启东中学作业本八年级数学上册苏科版盐城专版》

1. (1)如图①,直线$m经过\triangle ABC的顶点A$,$AB = AC$,在直线$m上取两点D$,$E$,使$∠ADB = ∠AEC = \alpha$,补充$∠BAC = $______α(用含$\alpha$的式子表示),可使得线段$BD$,$CE与DE之间满足BD + CE = DE$,补充条件后证明；
(2)在(1)的$\triangle ABC$中,使$∠BAC = \beta$,将直线$m绕着点A$按逆时针方向旋转一个角度到如图②所示的位置,并改变条件$∠ADB = ∠AEC = $______180°−β(用含$\beta$的式子表示),通过观察或测量,猜想线段$BD$,$CE与DE$之间满足的数量关系,并予以证明。

答案： 1.解:
(1)α 证明:
∵∠ADB=∠BAC=α，
∴∠DBA+∠BAD=∠BAD+∠CAE=180°−α，
∴∠CAE=∠ABD.
　在△ADB和△CEA中，∠ADB=∠CEA，
　∠ABD=∠CAE，
　AB=CA，
∴△ADB≌△CEA(AAS)，
∴BD=AE，AD=CE，
∴BD+CE=AE+AD=DE;
(2)180°−β
　线段BD，CE与DE之间满足的数量关系为BD+DE=CE.证明:
∵∠ADB=180°−β，
∴∠ABD+∠BAD=β.
∵∠BAC=∠BAD+∠CAE=β，
∴∠ABD=∠CAE.
　在△ABD和△CAE中，∠ADB=∠CEA，
　∠ABD=∠CAE，
　AB=CA，
∴△ABD≌△CAE(AAS)，
∴BD=AE，AD=CE，
∴BD+DE=AE+DE=AD=CE.

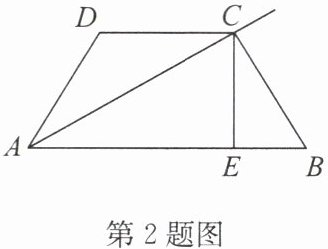
2. 如图,在四边形$ABCD$中,$AC平分∠BAD$,$CE⊥AB于点E$,$∠B + ∠D = 180^{\circ}$。求证：$AE = AD + BE$。

答案：
2.证明:过点C作CH⊥AD，交AD的延长线于点H，如答图，则∠CHA=90°.
∵AC平分∠BAD，CE⊥AB，
∴∠BAC=∠DAC，∠CEB=∠CEA=90°.
　在△AHC和△AEC中，∠CAH=∠CAE，
　∠H=∠CEA，
　AC=AC，
∴△AHC≌△AEC(AAS)，
∴CH=CE，AH=AE;
∵∠B+∠ADC=180°，∠CDH+∠ADC=180°，
∴∠CDH=∠B.
　在△CDH和△CBE中，∠CDH=∠B，
　∠CHD=∠CEB，
　CH=CE，
∴△CDH≌△CBE(AAS)，
∴BE=DH，
∴AE=AH=AD+DH=AD+BE.