《2025年启东中学作业本八年级数学上册苏科版盐城专版》

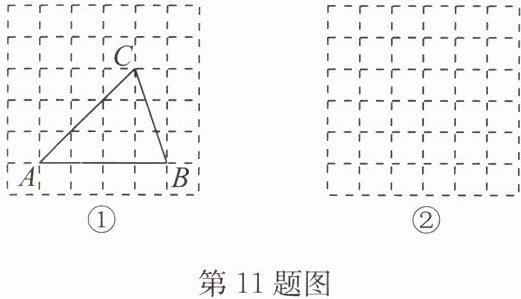
11.(10分)正方形网格中的每一个小正方形的边长都是1,每个小格的顶点叫作格点.
(1)如图①,以格点为顶点的$\triangle ABC$中,请判断$AB,BC,AC$三边的长度是有理数还是无理数；
(2)在图②中,以格点为顶点画一个三角形,使三角形的三边长分别为$3,\sqrt{5},\sqrt{8}$.

答案：
(1)解：由图①可知，AB在水平方向，长度为4个小正方形边长，所以AB=4，是有理数；
AC的长度，横向距离为3，纵向距离为2，根据勾股定理，AC=$\sqrt{3^{2}+2^{2}}=\sqrt{13}$，是无理数；
BC的长度，横向距离为1，纵向距离为2，根据勾股定理，BC=$\sqrt{1^{2}+2^{2}}=\sqrt{5}$，是无理数。
(2)解：（画图略，在图②中，例如取格点D(0,0)，E(3,0)，F(1,2)，则DE=3，DF=$\sqrt{1^{2}+2^{2}}=\sqrt{5}$，EF=$\sqrt{(3 - 1)^{2}+(0 - 2)^{2}}=\sqrt{8}$）

12.(10分)若$\sqrt{35}的整数部分为a$,6是$b$的算术平方根,求$3a-\frac{b}{2}-5$的立方根.

答案： 【解析】：
本题主要考察平方根、算术平方根、整数部分以及立方根的计算。
首先，我们需要确定$\sqrt{35}$的整数部分$a$。
由于$5^2 = 25 ＜ 35 ＜ 6^2 = 36$，
根据平方数的性质，我们可以得出$5 ＜ \sqrt{35} ＜ 6$。
因此，$\sqrt{35}$的整数部分$a = 5$。
接着，根据题目条件，$6$是$b$的算术平方根。
由算术平方根的定义，我们可以得出$b = 6^2 = 36$。
最后，我们需要求$3a - \frac{b}{2} - 5$的立方根。
将$a = 5$和$b = 36$代入表达式，得到：
$3a - \frac{b}{2} - 5 = 3 × 5 - \frac{36}{2} - 5 = 15 - 18 - 5 = -8$
因此，$3a - \frac{b}{2} - 5$的立方根是$\sqrt[3]{-8} = -2$。
【答案】：
$-2$

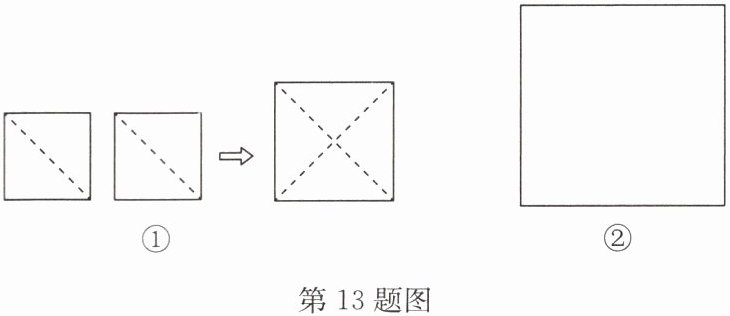
13.(15分)【问题发现】如图①,把两个面积都为$1\mathrm{cm}^{2}$的小正方形分别沿对角线剪开,将所得的4个直角三角形拼成一个大正方形,则该大正方形的边长为$\sqrt{2}$$\mathrm{cm}$.
【知识迁移】若一个圆与一个正方形的面积都是$2\pi\mathrm{cm}^{2}$,设这个圆的周长为$C_{圆}$,这个正方形的周长为$C_{正}$,则$C_{圆}$$＜$$C_{正}$.(填“$＞$”“$＜$”或“$=$”)
【拓展延伸】小明想用一块面积为$400\mathrm{cm}^{2}$的正方形纸片(如图②所示),沿着边的方向截出一块面积为$300\mathrm{cm}^{2}$的长方形纸片,使它的长、宽之比为$5:4$. 小明能用这块纸片裁出符合要求的纸片吗？请说明理由.

解：设长方形纸片的长为$5x\ \text{cm}$，宽为$4x\ \text{cm}$.
由题意，得$5x\cdot4x=300$，解得$x=\sqrt{15}$（负值舍去）.
$\therefore$长方形纸片的长为$5\sqrt{15}\ \text{cm}$.
$\because$正方形纸片的面积为$400\ \text{cm}^2$，$\therefore$其边长为$20\ \text{cm}$.
$\because 5\sqrt{15}\approx5×3.873=19.365＜20$，$\therefore$小明能用这块纸片裁出符合要求的纸片.

答案： 【问题发现】$\sqrt{2}$
【知识迁移】$＜$
【拓展延伸】解：设长方形纸片的长为$5x\ \text{cm}$，宽为$4x\ \text{cm}$.
由题意，得$5x\cdot4x=300$，解得$x=\sqrt{15}$（负值舍去）.
$\therefore$长方形纸片的长为$5\sqrt{15}\ \text{cm}$.
$\because$正方形纸片的面积为$400\ \text{cm}^2$，$\therefore$其边长为$20\ \text{cm}$.
$\because 5\sqrt{15}\approx5×3.873=19.365＜20$，$\therefore$小明能用这块纸片裁出符合要求的纸片.