第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1. (2024·资阳)若$\sqrt{5}\lt m<\sqrt{10}$,则整数$m$的值为 (
A.2
B.3
C.4
D.5
B
)A.2
B.3
C.4
D.5
答案:
B
2. (2024·南充)如图,数轴上表示$\sqrt{2}$的点是 (
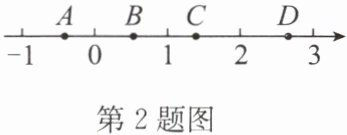
A.点$A$
B.点$B$
C.点$C$
D.点$D$
C
)
A.点$A$
B.点$B$
C.点$C$
D.点$D$
答案:
C
3. (2024·山西)比较大小:$\sqrt{6}$
>
2. (填“$>$”“$<$”或“$=$”)
答案:
>
4. (2024·滨州)写出一个比$\sqrt{3}$大且比$\sqrt{10}$小的整数:
2
.
答案:
2(答案不唯一)
5. 计算:(1)$\sqrt{16}-\sqrt[3]{27}$; (2)$2^{3}-\sqrt{4}+(\frac{2}{3}-\pi)^{0}$;
(3)$|-\sqrt{3}|-(4-\pi)^{0}+(\frac{1}{4})^{-1}$; (4)$(-1)^{2025}+(-\frac{1}{2})^{-2}-\sqrt{25}+\sqrt[3]{-27}$.
(3)$|-\sqrt{3}|-(4-\pi)^{0}+(\frac{1}{4})^{-1}$; (4)$(-1)^{2025}+(-\frac{1}{2})^{-2}-\sqrt{25}+\sqrt[3]{-27}$.
答案:
解:
(1)原式=4 - 3=1.
(2)原式=8 - 2+1=7.
(3)原式=$\sqrt{3}-1+4=3+\sqrt{3}$.
(4)原式=-1+4 - 5 - 3=-5.
(1)原式=4 - 3=1.
(2)原式=8 - 2+1=7.
(3)原式=$\sqrt{3}-1+4=3+\sqrt{3}$.
(4)原式=-1+4 - 5 - 3=-5.
6. 设$m= -\sqrt{20}$,则实数$m$所在的范围是 (
A.$m<-5$
B.$-5\lt m<-4$
C.$-4\lt m<-3$
D.$m>-3$
B
)A.$m<-5$
B.$-5\lt m<-4$
C.$-4\lt m<-3$
D.$m>-3$
答案:
B
7. 如图,直径为2个单位长度的圆从原点出发,沿数轴向右无滑动地滚动一周滚到了点$A$处,则点$A$表示的数是 (

A.$2\pi$
B.2
C.$\pi$
D.$\frac{\pi}{2}$
A
)
A.$2\pi$
B.2
C.$\pi$
D.$\frac{\pi}{2}$
答案:
A
8. 规定$(a)表示小于a$的最大整数,如$(3)= 2$,$(\sqrt{10})= 3$. 现将37进行如下操作:$37\overset{第一次}{\to}(\sqrt{37})= 6\overset{第二次}{\to}(\sqrt{6})= 2\overset{第三次}{\to}(\sqrt{2})= 1$. 类似地,只需要进行4次操作,就能变成1的所有正整数中,最小的正整数为______
677
.
答案:
677
9. 如图,数轴上的点$A$,$B$,$O$,$C$,$D分别表示数-2$,$-1$,$0$,$1$,$2$,则表示数$\sqrt{21}-5$的点应落在相邻两点
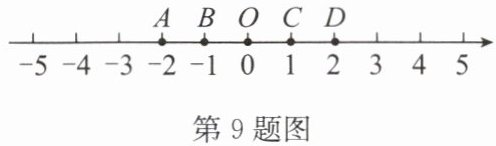
B,O
之间.
答案:
B,O
查看更多完整答案,请扫码查看


