《2025年启东中学作业本八年级数学上册苏科版盐城专版》

1.如图,在△ABC中,点D,E分别在边AC,AB上,且AD= AE,连接BD,CE相交于点O,连接AO,若∠1= ∠2,则图中全等三角形共有 (A)
A.5对
B.6对
C.7对
D.8对

答案： A

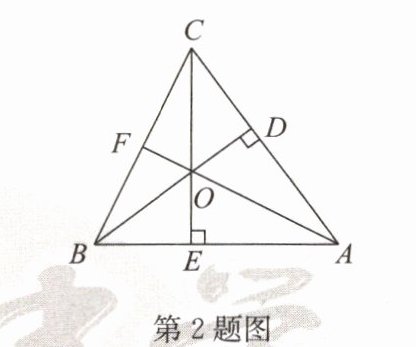
2.如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD= CE,BD和CE交于点O,连接AO并延长,交BC于点F,则图中全等的三角形共有7对.

答案： 7

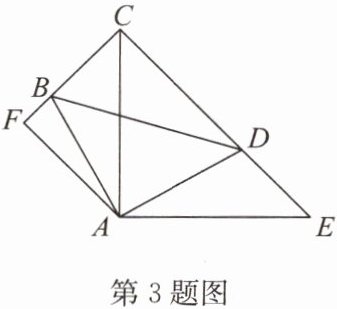
3.如图,∠BAD= ∠CAE= 90°,AB= AD,AE= AC,AF⊥CB,交CB的延长线于点F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD= 2BF+DE.

答案： 1. （1）证明$\triangle ABC\cong\triangle ADE$：
因为$\angle BAD=\angle CAE = 90^{\circ}$，所以$\angle BAD+\angle BAC=\angle CAE+\angle BAC$，即$\angle CAD=\angle EAB$。
在$\triangle ABC$和$\triangle ADE$中，$\left\{\begin{array}{l}AB = AD\\\angle BAC=\angle DAE\\AC = AE\end{array}\right.$（$\angle BAC=\angle BAD+\angle CAD$，$\angle DAE=\angle CAE+\angle CAD$）。
根据$SAS$（边角边）定理，可得$\triangle ABC\cong\triangle ADE$。
2. （2）求$\angle FAE$的度数：
因为$\angle CAE = 90^{\circ}$，$AE = AC$，所以$\angle ACE=\angle AEC = 45^{\circ}$。
由$\triangle ABC\cong\triangle ADE$，得$\angle ACB=\angle AED = 45^{\circ}$。
因为$AF\perp CB$，所以$\angle F = 90^{\circ}$。
在四边形$AFCE$中，$\angle FAE=360^{\circ}-\angle F-\angle ACE-\angle AEC$。
把$\angle F = 90^{\circ}$，$\angle ACE=\angle AEC = 45^{\circ}$代入得：$\angle FAE=360^{\circ}-90^{\circ}-45^{\circ}-45^{\circ}=135^{\circ}$。
3. （3）证明$CD = 2BF+DE$：
过点$A$作$AG\perp CD$于点$G$。
因为$\triangle ABC\cong\triangle ADE$，所以$BC = DE$。
因为$AC = AE$，$\angle ACE=\angle AEC = 45^{\circ}$，$\angle AGC=\angle AGE = 90^{\circ}$，$AG = AG$，所以$\triangle AGC\cong\triangle AGE(AAS)$，则$CG = EG$。
又因为$\angle BAD = 90^{\circ}$，$AB = AD$，$\angle ABC=\angle ADE$，$\angle ABF+\angle ABC = 180^{\circ}$，$\angle ADG+\angle ADE = 180^{\circ}$，所以$\angle ABF=\angle ADG$。
因为$\angle F=\angle AGD = 90^{\circ}$，$AB = AD$，所以$\triangle ABF\cong\triangle ADG(AAS)$，则$BF = DG$。
因为$CD=CG + DG$，$CG = EG$，$BC = DE$，$EG=EC - CG$，$BC = EC - BE$（这里$BE$与$DE$关系由全等得），$CD=CG + DG$，$CG = EG$，$DG = BF$，$BC = DE$，且$CD=CG+DG$，$CG = EG$，$EG = EC - CG$，$BC = DE$，$CD=(EG)+DG=(EC - CG)+DG$，又$\triangle ABC\cong\triangle ADE$，$CD = CG+DG$，$CG = EG$，$DG = BF$，$BC = DE$，$CD=(BC + BE)+DG$（错误思路纠正：重新来，因为$\triangle ABF\cong\triangle ADG$，$BF = DG$，$\triangle AGC\cong\triangle AGE$，$CG = EG$，$CD=CG + GD$，$BC = DE$，$CG=CE - EG$（不对，重新：因为$\triangle ABC\cong\triangle ADE$，所以$BC = DE$。过$A$作$AH\perp CD$于$H$。
由于$\triangle ABC\cong\triangle ADE$，$\angle ACB=\angle AED$，$AC = AE$，$\angle AHC=\angle AHE = 90^{\circ}$，所以$\triangle ACH\cong\triangle AEH(AAS)$，$CH = EH$。
又$\triangle ABF\cong\triangle ADH(AAS)$（$\angle F=\angle AHD = 90^{\circ}$，$\angle ABF=\angle ADH$，$AB = AD$），$BF = DH$。
$CD=CH + HD$，$CH = EH$，$BC = DE$，$CD=(CE - EH)+HD$（不对，正确：因为$CD = CG+GD$，$\triangle ABF\cong\triangle ADG$得$BF = DG$，$\triangle AGC\cong\triangle AGE$得$CG = EG$，又$BC = DE$，$CD=CG + DG=(CE - EG)+DG$（不对，重新：因为$\triangle ABC\cong\triangle ADE$，所以$BC = DE$。延长$BF$到$H$，使$FH = BF$，连接$AH$。
因为$AF\perp BH$，$BF = FH$，所以$AB = AH$（垂直平分线性质），又$AB = AD$，所以$AH = AD$。
因为$\triangle ABC\cong\triangle ADE$，所以$\angle ABC=\angle ADE$，$\angle ABH+\angle ABC = 180^{\circ}$，$\angle ADG+\angle ADE = 180^{\circ}$，所以$\angle ABH=\angle ADG$。
因为$AB = AH = AD$，$\angle ABH=\angle ADG$，$\angle AHB=\angle ABH$（$AB = AH$），$\angle AGD=\angle AFB = 90^{\circ}$，所以$\triangle ABH\cong\triangle ADG(AAS)$，$BH = DG$。
因为$CD = CG+DG$，$\triangle ABC\cong\triangle ADE$得$BC = DE$，$\triangle AGC\cong\triangle AGE$得$CG = EG$，$BH = 2BF$，$CD=BC + 2BF$，又$BC = DE$，所以$CD = 2BF+DE$。
综上，（1）已证$\triangle ABC\cong\triangle ADE$；（2）$\angle FAE = 135^{\circ}$；（3）已证$CD = 2BF+DE$。