第101页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
7. (2024·崇川区月考)下列曲线中不能表示$y$是$x$的函数的是(
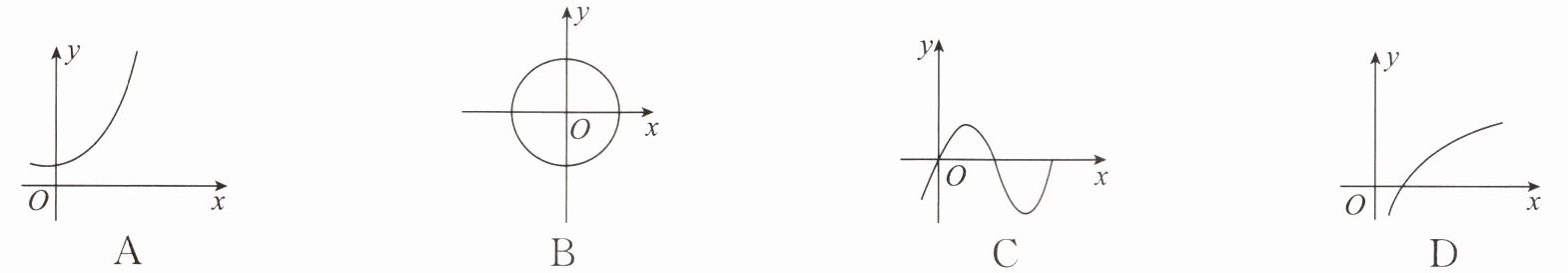
B
)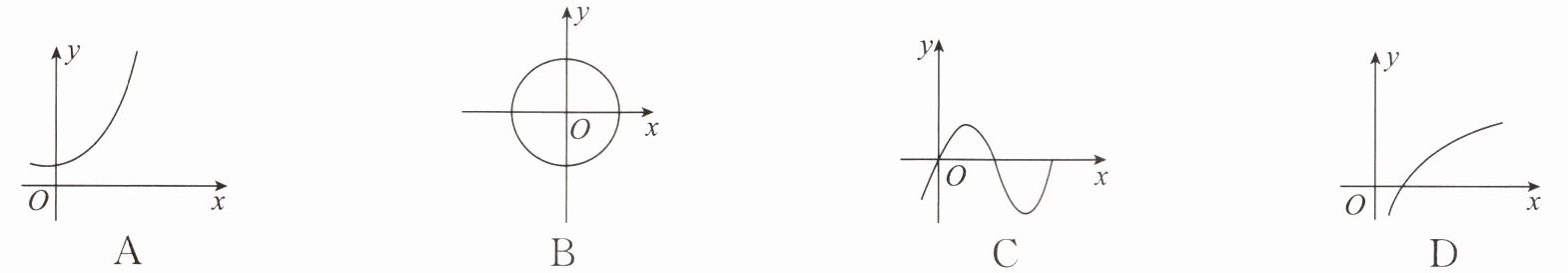
答案:
B
8. 小高从家骑车去单位上班,先走平路到达点$A$,再走上坡路到达点$B$,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家需要的时间是____
15
____分钟.
答案:
15
9. 小红帮弟弟荡秋千,秋千离地面的高度$h$(m)与摆动时间$t$(s)之间的关系如图所示.
(1)根据函数的定义,请判断变量$h$是否为关于$t$的函数.
(2)结合图象解答下列问题:
①当$t=0.7s$时,$h$的值是多少?并说明它的实际意义;
②秋千摆动第一个来回需要多少秒?
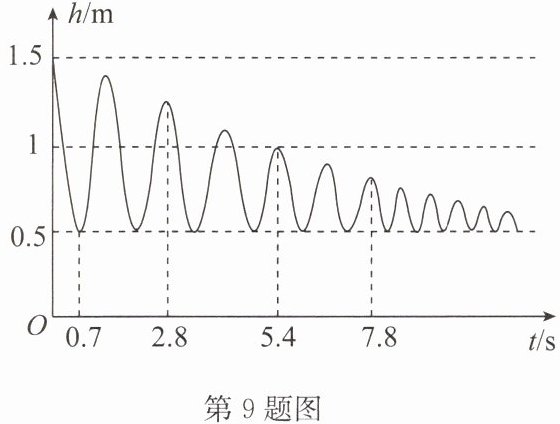
(1)根据函数的定义,请判断变量$h$是否为关于$t$的函数.
(2)结合图象解答下列问题:
①当$t=0.7s$时,$h$的值是多少?并说明它的实际意义;
②秋千摆动第一个来回需要多少秒?

答案:
解:
(1)
∵对于每一个摆动时间t,h都有唯一的值与其对应,
∴变量h是关于t的函数.
(2)①$h=0.5\ \text{m}$,它的实际意义是秋千摆动0.7 s时,离地面的高度为0.5 m.
②秋千摆动第一个来回需要2.8 s.
(1)
∵对于每一个摆动时间t,h都有唯一的值与其对应,
∴变量h是关于t的函数.
(2)①$h=0.5\ \text{m}$,它的实际意义是秋千摆动0.7 s时,离地面的高度为0.5 m.
②秋千摆动第一个来回需要2.8 s.
10. 如图①,底面积为$30cm^{2}$的空圆柱形容器内水平放置着由两个实心圆柱组成的“几何体”.现向容器内匀速注水,注满为止.在注水过程中,水面高度$h$(cm)与注水时间$t$(s)之间的关系如图②所示.
请根据图中提供的信息解答下列问题:
(1)圆柱形容器的高为
(2)若“几何体”下方圆柱的底面积为$15cm^{2}$,求“几何体”上方圆柱的高和底面积.
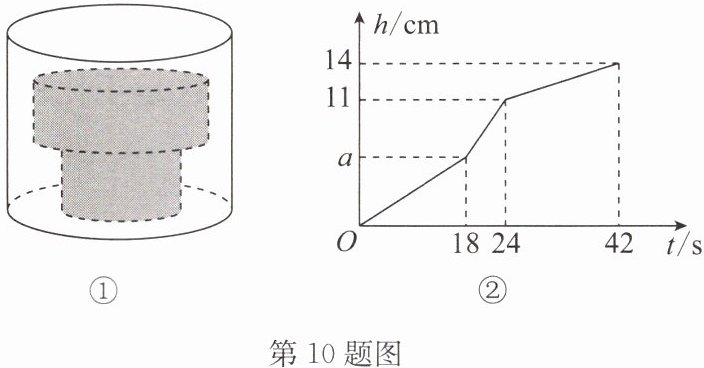
请根据图中提供的信息解答下列问题:
(1)圆柱形容器的高为
14
cm,匀速注水的水流速度为5
$cm^{3}/s$;(2)若“几何体”下方圆柱的底面积为$15cm^{2}$,求“几何体”上方圆柱的高和底面积.

解:由题意可知,$30a-15a=18× 5$,解得$a=6$.故"几何体"上方圆柱的高为$11-6=5(\text{cm})$.设"几何体"上方圆柱的底面积为$S\ \text{cm}^2$,则$(30-S)× 5=5× (24-18)$,解得$S=24$.故"几何体"上方圆柱的底面积为$24\ \text{cm}^2$.
答案:
(1)14 5
(2)解:由题意可知,$30a-15a=18× 5$,解得$a=6$.
故"几何体"上方圆柱的高为$11-6=5(\text{cm})$.
设"几何体"上方圆柱的底面积为$S\ \text{cm}^2$,
则$(30-S)× 5=5× (24-18)$,解得$S=24$.
故"几何体"上方圆柱的底面积为$24\ \text{cm}^2$.
(1)14 5
(2)解:由题意可知,$30a-15a=18× 5$,解得$a=6$.
故"几何体"上方圆柱的高为$11-6=5(\text{cm})$.
设"几何体"上方圆柱的底面积为$S\ \text{cm}^2$,
则$(30-S)× 5=5× (24-18)$,解得$S=24$.
故"几何体"上方圆柱的底面积为$24\ \text{cm}^2$.
查看更多完整答案,请扫码查看


