《2025年启东中学作业本八年级数学上册苏科版盐城专版》

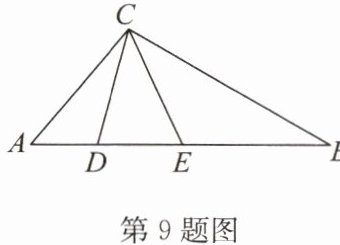
9.(2024·内江)如图,在$\triangle ABC$中,$∠DCE= 40^{\circ },AE= AC,BC= BD$,则$∠ACB$的度数为______100°.

答案： 100°

10.如图,$∠BOC= 9^{\circ }$,点A在OB上,且$OA= 1$,按下列要求画图:以点A为圆心,1为半径向右画弧交OC于点$A_{1}$,连接$AA_{1}$,得第1条线段$AA_{1}$;再以点$A_{1}$为圆心,1为半径向右画弧交OB于点$A_{2}$,连接$A_{1}A_{2}$,得第2条线段$A_{1}A_{2}$;再以点$A_{2}$为圆心,1为半径向右画弧交OC于点$A_{3}$,连接$A_{2}A_{3}$,得第3条线段$A_{2}A_{3}$;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则$n= $9.

答案： 9

11.已知,在$\triangle ABC$中,$AB= AC,∠BAC= 45^{\circ }$.
(1)如图,点D在AB边上,点E在AC边上,$BD= CE$,BE与CD交于点F.求证:$∠ABE= ∠ACD;$
(2)若D是AB边上的一个动点,E是AC边上的一个动点,且$BD= CE$,BE与CD交于点F.当$\triangle BFD$是等腰三角形时,求$∠FBD$的度数.

答案：
(1)证明:
∵AB=AC,
∴∠ABC=∠ACB.
在△BCD与△CBE中,{BC=CB,∠DBC=∠ECB,BD=CE,
∴△BCD≌△CBE(SAS),
∴∠FBC=∠FCB,
∴∠ABC - ∠FBC=∠ACB - ∠FCB,即∠ABE=∠ACD.
(2)解:
∵AB=AC,∠BAC=45°,
∴∠ABC=∠ACB= $\frac{1}{2}$(180° - ∠BAC)=67.5°.设∠FBD=∠ECF=x,则∠FBC=∠FCB=67.5° - x,∠BDF=∠ECF+∠BAC=x+45°,∠DFB=2∠FBC=2(67.5° - x)=135° - 2x.
∵△BFD是等腰三角形,
∴BD=BF或BD=DF或BF=DF.①当BD=BF时,∠BDF=∠DFB,
∴x+45°=135° - 2x,解得x=30°,即∠FBD=30°;②当BD=DF时,∠FBD=∠DFB,
∴x=135° - 2x,解得x=45°,即∠FBD=45°;③当BF=DF时,∠FBD=∠FDB,
∴x=x+45°,无解，舍去.综上,∠FBD的度数为30°或45°.

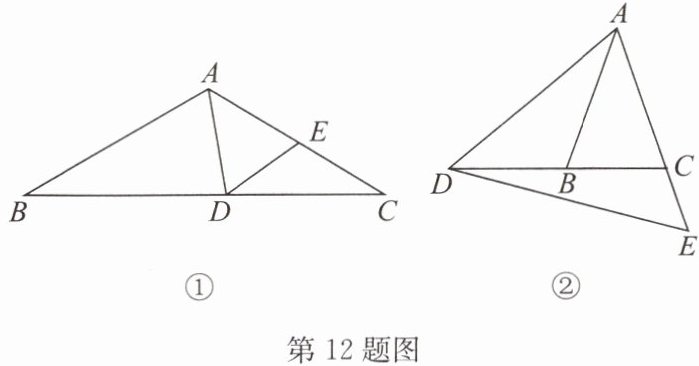
12.如图,在$\triangle ABC$中,$∠ABC= ∠ACB$,点D在直线BC上,点E在射线AC上,连接DE,$∠ADE= ∠AED$.
(1)如图①,若$∠B= ∠C= 30^{\circ },∠BAD= 70^{\circ }$,求$∠CDE$的度数;
(2)如图②,若$∠ABC= ∠ACB= 70^{\circ },∠CDE= 15^{\circ }$,求$∠BAD$的度数;
(3)当点D在直线BC上(不与点B,C重合)运动时,试探究$∠BAD与∠CDE$的数量关系,并说明理由.

答案：

(1)
∵∠B=∠C=30°,
∴∠BAC=120°.
∵∠BAD=70°,
∴∠DAE=50°,
∴∠ADE=∠AED=65°,
∴∠CDE=∠AED - ∠C=65° - 30°=35°.
(2)
∵∠ACB=70°,∠CDE=15°,
∴∠E=70° - 15°=55°,
∴∠ADE=∠AED=55°,
∴∠ADC=40°.
∵∠ABC=∠ADB+∠DAB=70°,
∴∠BAD=30°.
(3)∠BAD=2∠CDE.理由:设∠ABC=∠ACB=y,∠ADE=∠AED=x,∠CDE=α,∠BAD=β.分以下三种情况讨论:

第一种情况,如答图①,当点D在点B的左侧时,∠ADC=x - α,
∴{y=x+α,y=x - α+β,两式相减,得2α - β=0,
∴2α=β;
第二种情况,如答图②,当点D在线段BC上时,∠ADC=x+α,
∴{x=y+α,x+α=y+β,两式相减,得α=β - α,
∴2α=β;
第三种情况,如答图③,当点D在点C的右侧时,∠ADC=x - α,
∴{x - α+y+β=180°,y+x+α=180°,两式相减,得2α - β=0,
∴2α=β.
综上所述,∠BAD与∠CDE的数量关系是∠BAD=2∠CDE.