《2025年启东中学作业本八年级数学上册苏科版盐城专版》

12.（12分）已知点$P(a - 2,2a + 8)$，分别根据下列条件求出点$P$的坐标.
（1）点$P$在$x$轴上；
（2）点$P$在$y$轴上；
（3）点$Q$的坐标为$(1,5)$，直线$PQ // y$轴；
（4）点$P$到$x$轴，$y$轴的距离相等.

答案： 解:
(1)根据题意，得2a+8=0,解得a=−4,
∴a−2=−4−2=−6,
∴P(−6,0).
(2)根据题意,得a−2=0,解得a=2,
∴2a+8=2×2+8=12,
∴P(0,12).
(3)根据题意,得a−2=1,解得a=3,
∴2a+8=2×3+8=14,
∴P(1,14).
(4)根据题意,得a−2=2a+8或a−2+2a+8=0,解得a=−10或a=−2. 当a=−10时,a−2=−10−2=−12,2a+8=2×(−10)+8=−12,
∴P(−12,−12); 当a=−2时,a−2=−2−2=−4,2a+8=2×(−2)+8=4,
∴P(−4,4). 综上所述,点P的坐标为(−12,−12)或(−4,4).

13.（10分）如图，在平面直角坐标系中，已知点$A(0,4)$，$B( - 3,0)$，连接$AB$.将$\triangle A O B$沿过点$B$的直线折叠，使点$A$落在$x$轴上的点$A ^ { \prime }$处，折痕交$y$轴于点$C$，求点$A ^ { \prime }$，$C$的坐标.

答案： 解:
∵A(0,4),B(−3,0),
∴OA=4,OB=3. 在Rt△OAB中,由勾股定理，得AB=5.
∵△AOB沿过点B的直线折叠，点A落在x轴上的点A'处，
∴BA'=BA=5,CA'=CA,
∴OA'=BA'−OB=5−3=2,
∴点A'的坐标为(2,0). 设OC=m,则CA'=CA=4−m. 在Rt△OCA'中,由勾股定理,得OC²+OA'²=CA'²,即m²+2²=(4−m)²,解得m=3/2,
∴点C的坐标为(0,3/2).

14.（16分）如图①，在平面直角坐标系中，直线$AB$分别交$y$轴，$x$轴于点$A(0,a)$，点$B(b,0)$，且$a$，$b$满足$a ^ { 2 } - 4 a + 4 + \sqrt { 2 b + 2 } = 0$.
（1）求$a$，$b$的值.
（2）如图②，以$AB$为直角边作$\mathrm { Rt } \triangle A B C$，点$C$落在第四象限且$\angle A C B = 45 ^ { \circ }$，求点$C$的坐标.
（3）在（2）的条件下，$AC$与$x$轴交于点$D$，$BC$与$y$轴交于点$E$，连接$DE$，过点$C$作$CF \perp BC$交$x$轴于点$F$.
①求证：$C F = \frac { 1 } { 2 } B C$；
②求点$C$到$DE$的距离.

答案：

(1)解:
∵a²−4a+4+√(2b+2)=0,
∴(a−2)²+√(2b+2)=0.
∵(a−2)²≥0,√(2b+2)≥0,
∴a−2=0,2b+2=0,解得a=2,b=−1.
(2)解:由
(1)知a=2,b=−1,
∴A(0,2),B(−1,0),
∴OA=2,OB=1.
∵△ABC是直角三角形，且∠ACB=45°，点C在第四象限，
∴∠ABC=90°,∠CAB=45°. 如答图①,过点C作CG⊥OB于点G,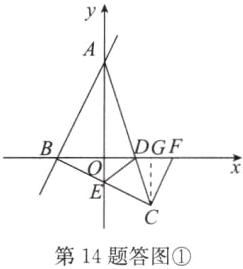
∵∠CAB=∠ACB,
∴AB=BC;
∵∠ABC=∠AOB=90°,
∴∠OAB+∠OBA=∠OBA+∠CBG=90°,
∴∠OAB=∠GBC,
∴△AOB≌△BGC,
∴CG=OB=1,BG=OA=2,
∴OG=1,
∴点C的坐标为(1,−1).
(3)①证明:如答图②,由
(2)知点C(1,−1), 过点C作CL⊥y轴于点L,则CL=1=BO. 在△BOE和△CLE中,{∠OEB=∠LEC,∠EOB=∠ELC,BO=CL,
∴△BOE≌△CLE(AAS),
∴BE=CE.
∵∠ABC=90°,
∴∠BAO+∠BEA=90°.
∵∠BOE=90°,
∴∠CBF+∠BEA=90°,
∴∠BAE=∠CBF.
∵CF⊥BC,
∴∠BCF=90°=∠ABC. 在△ABE和△BCF中,{∠BAE=∠CBF,AB=BC,∠ABE=∠BCF,
∴△ABE≌△BCF(ASA),
∴BE=CF,
∴CF=1/2BC. ②解:如答图③,过点C作CK⊥ED于点K,CG⊥DF于点G,由①知BE=CF.
∵BE=CE=1/2BC,
∴CE=CF.
∵∠ACB=45°,∠BCF=90°,
∴∠ECD=∠DCF.
∵DC=DC,
∴△CDE≌△CDF(SAS),
∴∠CDE=∠CDF,
∴CK=CG=1,
∴点C到DE的距离为1.