《2025年启东中学作业本八年级数学上册苏科版盐城专版》

6.将一根长为24cm的筷子置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是(D)
A.$h≤17$
B.$h≥8$
C.$15≤h≤16$
D.$7≤h≤16$

答案： D

7.如图,在垂直于地面的墙上离地面4m的点A斜放一架长5m的梯子,由于摆放不小心,梯子在墙上下滑1m到点$A'$处,则梯子在地面上滑出的距离$BB'$是1m.

答案： 1

8.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙脚的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为2.2米.

答案： 2.2

9.如图,在一条东西走向的河一侧有一村庄C,河边原有两个取水点A,B,其中$AB= AC$,由于某种原因,由C到A的路现在已经不通,C村为方便村民取水,决定在河边新建一个取水点H(点A,H,B在一条直线上),并新修一条路CH,测得$CB= 3$千米,$CH= 2.4$千米,$HB= 1.8$千米.
(1)问CH是否为从村庄C到河边最近的路?请通过计算加以说明.
(2)求原来的路线AC的长.

答案： 解:
(1)是,理由:在△CHB中,
∵$CH^{2}+BH^{2}=2.4^{2}+1.8^{2}=9$,$BC^{2}=9$,
∴$CH^{2}+BH^{2}=BC^{2}$,
∴CH⊥AB,
∴CH是从村庄C到河边最近的路.
(2)在Rt△ACH中,设AC=AB=x千米,则AH=(x - 1.8)千米,由勾股定理，得$AC^{2}=AH^{2}+CH^{2}$,
∴$x^{2}=(x−1.8)^{2}+2.4^{2}$,解得x=2.5.答:原来的路线AC的长为2.5千米.

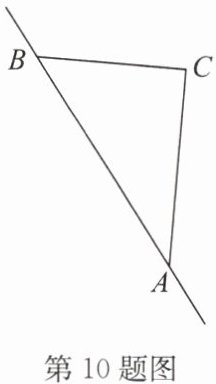
10.如图,有一辆环卫车沿公路AB由点A向点B行驶,已知点C为一所学校,且点C与直线AB上两点A,B的距离分别为200m和150m,$AB= 250m$,环卫车周围130m以内为受噪声影响区域.
(1)学校C会受噪声影响吗?为什么?
(2)若环卫车噪声影响该学校持续的时间为2min,求环卫车行驶的速度.

答案： 解:
(1)学校C会受噪声影响，理由:如答图，过点C作CD⊥AB于点D.
∵AC=200m,BC=150m,AB=250m,
∴$AC^{2}+BC^{2}=AB^{2}$,
∴△ABC是直角三角形,∠ACB=90°,
∴$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}CD\cdot AB$,
∴$CD=\frac{200×150}{250}=120$.
∵环卫车周围130m以内为受噪声影响区域,
∴学校C会受噪声影响.
(2)如答图,在AB上取点E,F,使EC=130m,FC=130m.
∵$ED=\sqrt{EC^{2}-CD^{2}}=\sqrt{130^{2}-120^{2}}=50(m)$,
∴EF=2ED=100(m).
∵环卫车噪声影响该学校持续的时间为2min,
∴环卫车行驶的速度为100÷2=50(m/min).答:环卫车行驶的速度为50m/min.