《2025年启东中学作业本八年级数学上册苏科版盐城专版》

1.【问题驱动】如何验证勾股定理及探究勾股数?
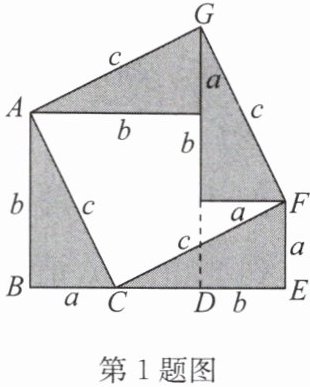
【活动操作】小明参照教材用 4 张全等的直角三角形纸片拼成如图所示的五边形 ABEFG.
【探索新知】
(1)从面积的角度思考,请用两种方法计算五边形 ABEFG 的面积,并写出得到等式$a^{2}+b^{2}=c^{2}$的过程;
(2)如果满足等式$a^{2}+b^{2}=c^{2}$的 a,b,c 是三个正整数,那么称 a,b,c 为勾股数.已知 m,n 是正整数且$m＞n$,证明:$2mn,m^{2}-n^{2},m^{2}+n^{2}$是勾股数;
【灵活运用】
(3)在如图所示的五边形 ABEFG 中,若$a=4,b=8$,则空白部分的面积为____;
(4)请写出任意一组含有 85 的勾股数:____;
(5)小明在他找到的勾股数的表达式中,用$2n^{2}+4n+4$(n 为任意正整数)表示勾股数中的最大的一个数,则另两个数是____,____.(用含 n 的式子表示)

答案：

(1)解:如答图.
　　　　　　　
　方法一:S五边形ABEFG=S正方形ABDN+S正方形MDEF+S△MFG+S△ANG=b²+a²+$\frac{1}{2}$ab+$\frac{1}{2}$ab=a²+b²+ab,
　方法二:S五边形ABEFG=S正方形ACFG+S△ABC+S△CEF=c²+$\frac{1}{2}$ab+$\frac{1}{2}$ab=c²+ab,
∴a²+b²+ab=c²+ab,
∴a²+b²=c².
(2)证明:
∵(2mn)²=4m²n²,(m²−n²)²=m⁴+n⁴−2m²n²,
∴(2mn)²+(m²−n²)²=4m²n²+m⁴+n⁴−2m²n²=(m²+n²)².
∵m,n是正整数且m＞n,
∴2mn,m²−n²,m²+n²都是正整数，
∴2mn,m²−n²,m²+n²是勾股数.
(3)48
(4)85,3612,3613(答案不唯一)
(5)2n²+4n　4n+4