《2025年课堂点睛八年级数学上册人教版》

5. 发现：任意三个连续偶数的平方和是 4 的倍数。
(1) $(-2)^{2}+0^{2}+2^{2}$的结果是 4 的几倍？
(2) 设三个连续偶数的中间一个数为 $2x$,写出它们的平方和,并说明是 4 的倍数；
(3) 任意三个连续数的平方和,被 3 除余数是几？设中间一个数为 $x$,请直接写出结果。

答案： 5.
(1)解:(-2)²+0²+2²=4+4=8,8÷4=2,
∴是4的2倍.
(2)若三个连续偶数的中间一个数为2x,则另外两个偶数分别为2x-2和2x+2,平方和为(2x-2)²+(2x)²+(2x+2)²=4x²-8x+4+4x²+4x²+8x+4=12x²+8=4(3x²+2),
∴其平方和是4的倍数.
(3)被3除余数是2.

6. “任意一个个位数字是 5 的自然数,平方后的末两位数(即十位数字和个位数字组成的两位数)一定是 25”。这一结论可用下面的方法进行证明。
解：设个位数字是 5 的自然数为 $10a + 5$($a$ 为自然数),则 $(10a + 5)^{2}= 100a^{2}+100a + 25 = 100(a^{2}+a)+25$。
这说明平方后的末两位数一定是 25。
请你探索下面的问题：“任意一个末两位数是 25 的自然数,平方后的末三位数(即依次由百位、十位和个位数字组成的三位数)一定是多少？”并给出证明。

答案： 6. 解:平方后的末三位数一定是625.证明:设末尾数字是25的自然数为100a+25(a为自然数),则(100a+25)²=10000a²+5000a+625=1000(10a²+5a)+625.这说明平方后的末三位数一定是625.

7. (数形结合)两个边长分别为 $a$ 和 $b$ 的正方形 ($a ＞ b$) 如图放置(图①②③),若阴影部分的面积分别记为 $S_{1}$,$S_{2}$,$S_{3}$。

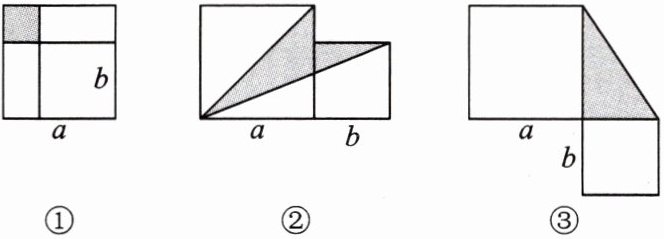
(1) 用含 $a$,$b$ 的式子分别表示 $S_{1}$,$S_{2}$,$S_{3}$；
(2) 若 $S_{1}= 1$,$S_{3}= 3$,则 $S_{2}$ 的值为____7/2；
(3) 若对于任意的正数 $a$,$b$,都有 $S_{1}+mS_{3}= kS_{2}$($m$,$k$ 为常数),求 $m$,$k$ 的值。
(1)解:S₁=(a-b)²;S₂=1/2a²-1/2ab+1/2b²;S₃=1/2ab.
(3)∵对于任意的正数a,b,都有S₁+mS₃= kS₂(m,k为常数),
∴(a-b)²+m(1/2ab)=k(1/2a²-1/2ab+1/2b²),整理得2(a²+b²)+ab(m-4)=(a²+b²)k+ab(-k).
∵m,k为常数,
∴由待定系数法得k=2,m-4=-k,解得m=2,k=2.

答案： 7.
(1)解:S₁=(a-b)²;S₂=1/2a²-1/2ab+1/2b²;S₃=1/2ab.
(2)7/2
(3)
∵对于任意的正数a,b,都有S₁+mS₃= kS₂(m,k为常数),
∴(a-b)²+m(1/2ab)=k(1/2a²-1/2ab+1/2b²),整理得2(a²+b²)+ab(m-4)=(a²+b²)k+ab(-k).
∵m,k为常数,
∴由待定系数法得k=2,m-4=-k,解得m=2,k=2.