《2025年课堂点睛八年级数学上册人教版》

9. 如图,点$E在等边\triangle ABC的边BC$上,$CE = 14$,射线$BD\perp CB于点B$,点$P是射线BD$上一动点,点$F是线段AC$上一动点,当$PE + PF$的值最小时,$CF = 9$,则$AB$的长为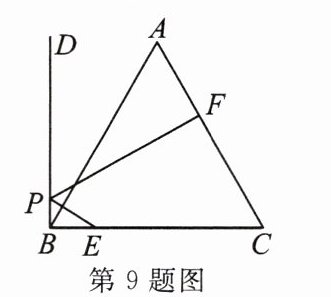16。

答案： 16

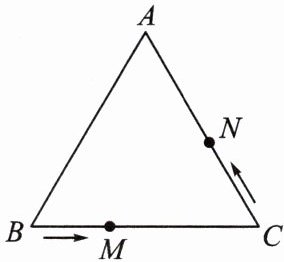
10. 如图,在$\triangle ABC$中,$AB = AC = BC = 6$,点$M$,$N分别是BC$,$CA$边上的动点。点$M从点B运动到点C$,点$N从点C运动到点A$,已知点$M的速度为每秒1$个单位长度,点$N的速度为每秒1.5$个单位长度,当其中一点到达终点时,另一点随之停止运动。设运动时间为$t\ s$,当$\triangle MCN$为直角三角形时,求$t$的值。

答案： 解：
∵AB=AC=BC=6，
∴△ABC是等边三角形，
∴∠C=60°，
∵△MCN为直角三角形，
∴∠NMC=90°或∠MNC=90°，①设运动时间为 t₁ s 时，∠NMC=90°，
∵∠C=60°，
∴∠CNM=30°，
∴2CM=CN，
∴2(6-t₁)=1.5t₁，解得 t₁=24/7；②设运动时间为 t₂ s 时，∠MNC=90°，
∵∠C=60°，
∴∠CMN=30°，
∴2CN=CM.
∴2×1.5t₂=6-t₂，解得 t₂=3/2.又
∵0≤t≤4，
∴经检验，t₁，t₂符合题意，综上所述，当△MCN为直角三角形时，t的值为24/7或3/2.

11.(新考法·综合与实践)某数学兴趣小组开展了一次活动,过程如下：设$\angle BAC= \theta(0^{\circ}＜\theta＜90^{\circ})$。现把小棒依次摆放在两射线之间,并使小棒两端分别在射线$AB$,$AC$上。
活动一：如图1所示,从点$A_1$开始,依次向右摆放小棒,使小棒在端点处互相垂直,$A_1A_2$为第1根小棒。
数学思考：
(1)小棒能无限摆下去吗？答：能。(填“能”或“不能”)
(2)设$AA_1 = A_1A_2 = A_2A_3$,则$\theta=$22.5$^{\circ}$。
活动二：如图2所示,从点$A_1$开始,用等长的小棒依次向右摆放,其中$A_1A_2$为第1根小棒,且$A_1A_2 = AA_1$。
数学思考：
(3)若已经摆放了3根小棒,则$\theta_3= $4θ；(用含$\theta$的式子表示)
(4)若只能摆放4根小棒,则$\theta$的范围是18°≤θ＜22.5°。

答案：
(1)能
(2)22.5
(3)4θ
(4)18°≤θ＜22.5°