《2025年课堂点睛八年级数学上册人教版》

7. 有一条以互相平行的直线 $ a $,$ b $ 为岸的河流,其两侧有村庄 $ A $ 和村庄 $ B $,现在要在河上建一座桥梁 $ MN $(桥与河岸垂直),使两村庄之间的距离最短,从作图痕迹上来看,正确的是(D)

答案： D

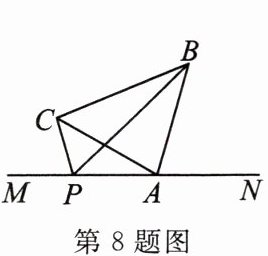
8. 如图,在 $ \triangle ABC $ 中,$ \angle CAB = 76^{\circ} $,$ AC = AB $,点 $ A $ 在直线 $ MN $ 上,$ \angle CAM = 30^{\circ} $,$ P $ 为直线 $ MN $ 上一动点,连接 $ CP $,$ BP $。当 $ CP + BP $ 的值最小时,$ \angle ACP $ 的度数为 $\underline{22°}$。

答案： 22°

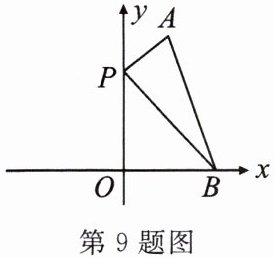
9. 如图,在平面直角坐标系中,点 $ A $,$ B $ 的坐标分别为 $ (2,6) $,$ (4,0) $,$ P $ 为 $ y $ 轴上一动点,且 $ A $,$ B $,$ P $ 三点不在同一条直线上,则当 $ \triangle ABP $ 周长最小时,点 $ P $ 的坐标为 $\underline{(0,4)}$。

答案： (0,4)

10. 如图,点 $ A $,$ B $ 在直线 $ l $ 的两侧,在直线 $ l $ 上求作一点 $ P $,使 $ |PA - PB| $ 的值最大。

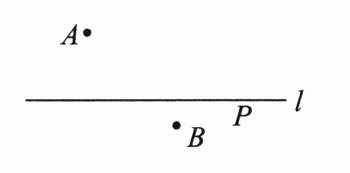
答案： 解:作点A关于直线l的对称点A'，连接A'B并延长交直线l于点P.

11. 茅坪民族中学八(2)班举行文艺晚会,桌子摆成如图所示两直排(图中的 $ AO $,$ BO $),$ AO $ 桌面上摆满了橘子,$ OB $ 桌面上摆满了糖果,站在 $ C $ 处的学生小明先拿橘子再拿糖果,然后到 $ D $ 处座位上,请你帮助他设计一条行走路线,使其所走的总路程最短。(保留作图痕迹,不写作法)

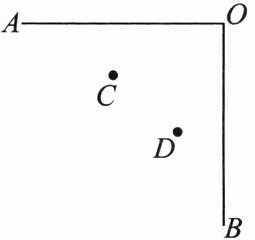
答案：
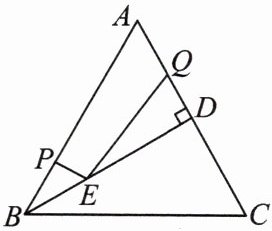
解:如图 ,小明沿C →P→Q→D的路线行走,所走的总路程最短.

12. 如图,在等边 $ \triangle ABC $ 中,$ BD \perp AC $ 于点 $ D $,点 $ P $,$ Q $ 分别为线段 $ AB $,$ AD $ 上的两个定点,且 $ QD = 15 $,$ BP = AQ = 20 $。
(1)作点 $ Q $ 关于直线 $ BD $ 对称的点 $ Q' $；
(2)在 $ BD $ 上有一动点 $ E $,求 $ PE + QE $ 的最小值。

答案：

(1)如图所示　　　　　　　 　　
(2)连接PQ'，EQ'.
∵△ABC为等边三角形，
∴AC=BA=BC，∠A=60°.
∵BD⊥AC，
∴AD=CD.
∵QD=Q'D，
∴CQ'=AQ=BP=20.
∴AP=AQ'=AQ+2QD=50.
∵∠A=60°，
∴△APQ'为等边三角形，
∴PQ'=AQ'=50.
∵PE+EQ=PE+EQ'≥PQ'=50，
∴当P，E，Q'三点共线时，PE+EQ取最小值50.