第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
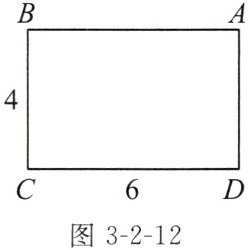
例1(教材典题)如图3-2-12,长方形ABCD的长与宽分别是6,4,建立适当的平面直角坐标系,写出各个顶点的坐标。
各个顶点的坐标为:A(

各个顶点的坐标为:A(
6,4
),B(0,4
),C(0,0
),D(6,0
)
答案:
【解析】:以点$C$为坐标原点,分别以$CD$,$CB$所在直线为$x$轴,$y$轴建立平面直角坐标系。
因为长方形$ABCD$中$CD = 6$,$CB = 4$,所以点$C$坐标为$(0,0)$;点$D$在$x$轴正半轴上,且$CD = 6$,所以$D$点坐标为$(6,0)$;点$B$在$y$轴正半轴上,且$CB = 4$,所以$B$点坐标为$(0,4)$;点$A$横坐标与$D$点横坐标相同为$6$,纵坐标与$B$点纵坐标相同为$4$,所以$A$点坐标为$(6,4)$。
【答案】:$A(6,4)$,$B(0,4)$,$C(0,0)$,$D(6,0)$
因为长方形$ABCD$中$CD = 6$,$CB = 4$,所以点$C$坐标为$(0,0)$;点$D$在$x$轴正半轴上,且$CD = 6$,所以$D$点坐标为$(6,0)$;点$B$在$y$轴正半轴上,且$CB = 4$,所以$B$点坐标为$(0,4)$;点$A$横坐标与$D$点横坐标相同为$6$,纵坐标与$B$点纵坐标相同为$4$,所以$A$点坐标为$(6,4)$。
【答案】:$A(6,4)$,$B(0,4)$,$C(0,0)$,$D(6,0)$
例2(教材典题)如图3-2-13,对于边长为4的等边三角形ABC,建立适当的平面直角坐标系,写出各个顶点的坐标。


答案:
解:如图,以边BC所在直线为x轴,以边BC的中垂线为y轴建立平面直角坐标系.
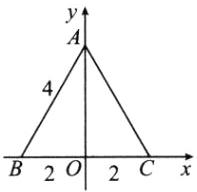
由等边三角形的性质可知,△ABO是直角三角形,所以AO=$\sqrt{AB^{2}-BO^{2}}=\sqrt{4^{2}-2^{2}}=2\sqrt{3}$.所以顶点A,B,C的坐标分别为A(0,2$\sqrt{3}$),B(-2,0),C(2,0).(答案不唯一,合理即可)
解:如图,以边BC所在直线为x轴,以边BC的中垂线为y轴建立平面直角坐标系.

由等边三角形的性质可知,△ABO是直角三角形,所以AO=$\sqrt{AB^{2}-BO^{2}}=\sqrt{4^{2}-2^{2}}=2\sqrt{3}$.所以顶点A,B,C的坐标分别为A(0,2$\sqrt{3}$),B(-2,0),C(2,0).(答案不唯一,合理即可)
例3(教材典题)如图3-2-14,在一次“寻宝”游戏中,寻宝人已经找到了A(3,2)和B(3,-2)两个标志点,并且知道藏宝地点的坐标为(4,4),除此之外不知道其他信息。如何确定平面直角坐标系找到“宝藏”?


取$AB$中点$C(3,0)$,过$C$作$AB$的垂线为$x$轴(向右为正方向),以$C$为起点,在$AB$上向上取长度为$3$个单位向左平移$3$个单位确定$y$轴(向上为正方向),建立平面直角坐标系,再根据坐标$(4,4)$找到“宝藏”。
答案:
【解析】:
1. 首先分析$A(3,2)$和$B(3, - 2)$的坐标特征:
两点横坐标相同,所以$AB$垂直于$x$轴。
计算$AB$的距离:$\vert2 - (-2)\vert=\vert2 + 2\vert = 4$。
取$AB$中点$C$,$C$点纵坐标为$\frac{2+( - 2)}{2}=0$,横坐标为$3$,即$C(3,0)$。
2. 然后确定$x$轴和$y$轴:
过$C$点作与$AB$垂直的直线为$x$轴(向右为正方向)。
以$C$点为起点,在$AB$上向上取长度为$3$个单位(因为$A$点纵坐标为$2$,$C$点纵坐标为$0$,$A$到$C$距离为$2$,这里根据坐标关系确定单位长度,$AB$距离为$4$,可看作$4$个单位长度,那么$1$个单位长度是$1$)向左平移$3$个单位长度确定$y$轴(向上为正方向)。
3. 最后根据建立的平面直角坐标系确定藏宝地点:
按照建立好的坐标系,根据坐标$(4,4)$找到“宝藏”位置。
【答案】:取$AB$中点$C(3,0)$,过$C$作$AB$的垂线为$x$轴(向右为正方向),以$C$为起点,在$AB$上向上取长度为$3$个单位向左平移$3$个单位确定$y$轴(向上为正方向),建立平面直角坐标系,再根据坐标$(4,4)$找到“宝藏”。
1. 首先分析$A(3,2)$和$B(3, - 2)$的坐标特征:
两点横坐标相同,所以$AB$垂直于$x$轴。
计算$AB$的距离:$\vert2 - (-2)\vert=\vert2 + 2\vert = 4$。
取$AB$中点$C$,$C$点纵坐标为$\frac{2+( - 2)}{2}=0$,横坐标为$3$,即$C(3,0)$。
2. 然后确定$x$轴和$y$轴:
过$C$点作与$AB$垂直的直线为$x$轴(向右为正方向)。
以$C$点为起点,在$AB$上向上取长度为$3$个单位(因为$A$点纵坐标为$2$,$C$点纵坐标为$0$,$A$到$C$距离为$2$,这里根据坐标关系确定单位长度,$AB$距离为$4$,可看作$4$个单位长度,那么$1$个单位长度是$1$)向左平移$3$个单位长度确定$y$轴(向上为正方向)。
3. 最后根据建立的平面直角坐标系确定藏宝地点:
按照建立好的坐标系,根据坐标$(4,4)$找到“宝藏”位置。
【答案】:取$AB$中点$C(3,0)$,过$C$作$AB$的垂线为$x$轴(向右为正方向),以$C$为起点,在$AB$上向上取长度为$3$个单位向左平移$3$个单位确定$y$轴(向上为正方向),建立平面直角坐标系,再根据坐标$(4,4)$找到“宝藏”。
1. 如图3-2-15是一只蝴蝶标本,已知表示蝴蝶两“翅膀尾部”A,B两点的坐标分别为(-2,-3),(2,-3),则表示蝴蝶身体“尾部”C点的坐标为(

A. (0,-1)
B. (1,-1)
C. (-1,0)
D. (2,-1)
A
)
A. (0,-1)
B. (1,-1)
C. (-1,0)
D. (2,-1)
答案:
A
2. 如图3-2-16,在△ABC中,AB=AC,BC=4,且BC边上的高为$\frac{3}{2}$,请你建立适当的平面直角坐标系,并写出A,B,C各点的坐标。


答案:
解:(答案不唯一)过点A作AO⊥BC于点O,
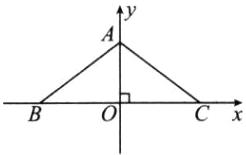
以BC所在直线为x轴,AO所在直线为y轴,建立如图所示的平面直角坐标系,则OA=$\frac{3}{2}$.因为AB=AC,所以OB=OC=$\frac{1}{2}$BC=2,所以A(0,$\frac{3}{2}$),B(-2,0),C(2,0).
解:(答案不唯一)过点A作AO⊥BC于点O,

以BC所在直线为x轴,AO所在直线为y轴,建立如图所示的平面直角坐标系,则OA=$\frac{3}{2}$.因为AB=AC,所以OB=OC=$\frac{1}{2}$BC=2,所以A(0,$\frac{3}{2}$),B(-2,0),C(2,0).
查看更多完整答案,请扫码查看


