第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
运用勾股定理解决实际问题时,要学会从实际问题中抽象出
直角
三角形模型,若没有可通过作垂直
来构建直角三角形模型.
答案:
直角 垂直
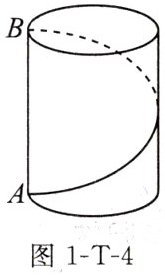
例4 核心素养 模型观念 葛藤是一种刁钻的植物,它的腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一手绝招,就是它绕树盘升的路线总是沿最短路线螺旋前进的,难道植物也懂数学?通过阅读以上信息,解决下列问题:
(1)若树干的周长(即图1-T-4中圆柱体的底面周长)为30cm,绕一圈升高(即圆柱的高)40cm,则它爬行一圈的路程是
(2)若树干的周长为80cm,爬行一圈的路程为100cm,爬行10圈到达树顶,则树干高
(1)若树干的周长(即图1-T-4中圆柱体的底面周长)为30cm,绕一圈升高(即圆柱的高)40cm,则它爬行一圈的路程是
50 cm
?(2)若树干的周长为80cm,爬行一圈的路程为100cm,爬行10圈到达树顶,则树干高
6 m
?
答案:
(1)50 cm
(2)6 m
(1)50 cm
(2)6 m
例5 新情境 日常生活 学习了勾股定理后,某校数学兴趣小组的同学把“测量风筝离地面的高度”作为一项课题活动,利用课余时间完成了实践调查,并形成如下活动报告:
| 活动报告 | |
| --- | --- |
| 课题 | 测量风筝离地面的高度 |
| 成员 | 组长:××× 组员:×××,×××,××× |
| 工具 | 皮尺等 |
| 示意图 | |
|
| 方案 | 如图1-T-5,先测量风筝到放风筝同学的水平距离BD,然后根据手中剩余风筝线的长度得出放出的风筝线长BF,最后测量握风筝线的手到地面的距离AB |
| 数据 | BD=16米,BF=20米,AB=1.7米 |
| 评价 | |
请根据活动报告回答下列问题:
(1)求此时风筝离地面的高度EF;
(2)若站在点A处不动,想把风筝从点F的位置竖直上升18米放到点C的位置,则还需放出风筝线多少米?
| 活动报告 | |
| --- | --- |
| 课题 | 测量风筝离地面的高度 |
| 成员 | 组长:××× 组员:×××,×××,××× |
| 工具 | 皮尺等 |
| 示意图 |
 |
|| 方案 | 如图1-T-5,先测量风筝到放风筝同学的水平距离BD,然后根据手中剩余风筝线的长度得出放出的风筝线长BF,最后测量握风筝线的手到地面的距离AB |
| 数据 | BD=16米,BF=20米,AB=1.7米 |
| 评价 | |
请根据活动报告回答下列问题:
(1)求此时风筝离地面的高度EF;
13.7 米
(2)若站在点A处不动,想把风筝从点F的位置竖直上升18米放到点C的位置,则还需放出风筝线多少米?
14 米
答案:
(1)13.7 米
(2)14 米
(1)13.7 米
(2)14 米
查看更多完整答案,请扫码查看


