第82页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
确定一次函数表达式的一般步骤是:先设出表达式$y=kx+b$,确定
两
个已知条件代入表达式求出$k,b$的值.
答案:
两
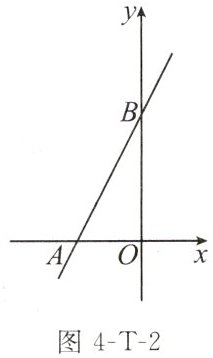
例3 如图4-T-2,在平面直角坐标系$xOy$中,已知点$A(-3,0),B(0,6)$.
(1)求直线$AB$对应的函数表达式;
(2)若$D$为坐标平面内一点,且$S_{△ABD}=15$,求所有的点$D$组成图形对应的函数表达式.
(1)求直线$AB$对应的函数表达式;
$y = 2x + 6$
(2)若$D$为坐标平面内一点,且$S_{△ABD}=15$,求所有的点$D$组成图形对应的函数表达式.
$y = 2x - 4$或$y = 2x + 16$

答案:
(1)$y = 2x + 6$
(2)$y = 2x - 4$或$y = 2x + 16$
(1)$y = 2x + 6$
(2)$y = 2x - 4$或$y = 2x + 16$
一般地,当一次函数$y=kx+b$的函数值为$0$时,相应的
自变量
的值就是方程$kx+b=0$的解.从图象上看,一次函数$y=kx+b$的图象与$x$轴交点的横
坐标就是方程$kx+b=0$的解.
答案:
自变量 横
例4 (1)如图4-T-3,直线$l$是一次函数$y=kx+b$的图象,点$A(-2,0),B(2,2)$在直线$l$上.请根据图象写出方程$kx+b=0$的解为

(2)已知关于$x$的方程$ax-b=1$的解为$x=-1$,则一次函数$y=ax-b-1$的图象与$x$轴交点的坐标为
$x = -2$
.
(2)已知关于$x$的方程$ax-b=1$的解为$x=-1$,则一次函数$y=ax-b-1$的图象与$x$轴交点的坐标为
$(-1, 0)$
.
答案:
(1)$x = -2$
(2)$(-1, 0)$
(1)$x = -2$
(2)$(-1, 0)$
例5 “生活即教育,行为即课程”.某校将劳动教育融入立德树人全过程.学校给每个班划分一块地供学生“种菜”,某班现要购买肥料对该地施肥,该班班长与农资店店主商量后,店主给出了两种购买方案(如下表),且都送货上门.
|方案|运费|肥料价格|
|----|----|----|
|方案一|15元|2.5元/kg|
|方案二|0元|3元/kg|
若该班购买$x\mathrm{k}\mathrm{g}$肥料,按方案一购买的付款总金额为$y_{1}$元,按方案二购买的付款总金额为$y_{2}$元.
(1)请分别写出$y_{1},y_{2}$与$x$之间的函数表达式;
(2)若该班计划用$180$元钱购买肥料,请问该班选择哪种购买方案购买的肥料较多.
|方案|运费|肥料价格|
|----|----|----|
|方案一|15元|2.5元/kg|
|方案二|0元|3元/kg|
若该班购买$x\mathrm{k}\mathrm{g}$肥料,按方案一购买的付款总金额为$y_{1}$元,按方案二购买的付款总金额为$y_{2}$元.
(1)请分别写出$y_{1},y_{2}$与$x$之间的函数表达式;
(2)若该班计划用$180$元钱购买肥料,请问该班选择哪种购买方案购买的肥料较多.
答案:
(1)$y_1 = 2.5x + 15$ $y_2 = 3x$
(2)方案一
(1)$y_1 = 2.5x + 15$ $y_2 = 3x$
(2)方案一
查看更多完整答案,请扫码查看


