《2025年全品学练考八年级数学上册北师大版深圳专版》

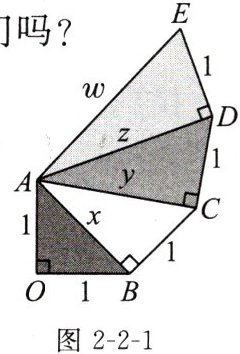
(1)根据图2-2-1填空：$x^{2}=$2，$y^{2}=$3，$z^{2}=$4，$w^{2}=$5。
(2)$x$，$y$，$z$，$w$中哪些是有理数？哪些是无理数？你能表示它们吗？

答案： 解:
(1)2 3 4 5
(2)z是有理数,x,y,w是无理数.$x=\sqrt{2}$,$y=\sqrt{3}$,$z=2$,$w=\sqrt{5}$.

算术平方根的概念：一般地，如果一个正数x的平方等于$a$，即$x^{2}=a$，那么这个正数x就叫作$a$的算术平方根，记作$\sqrt {a}$，读作“根号$a$”。
特别地，我们规定：0的算术平方根是0，即$\sqrt {0}=0$。

答案： 正数x的平方 正数x

例1(教材典题)求下列各数的算术平方根：
(1)900； (2)1； (3)$\frac {49}{64}$； (4)14。

答案：
(1)30
(2)1
(3)$\frac{7}{8}$
(4)$\sqrt{14}$

变式1 求下列各数的算术平方根：
(1)0.36； (2)$1\frac {7}{9}$； (3)$(-4)^{2}$； (4)$10^{-2}$。

答案：
(1)0.6
(2)$\frac{4}{3}$
(3)4
(4)$10^{-1}$

变式2 求下列各式的值：
(1)$\sqrt {81}$； (2)$\sqrt {\frac {64}{25}}$； (3)$\sqrt {0.04}$； (4)$-\sqrt {5^{2}-4^{2}}$。

答案：
(1)9
(2)$\frac{8}{5}$
(3)0.2
(4)-3

(1)在上面例1中，一些数的算术平方根的结果没有“$\sqrt {}$”了，这些数有什么特点？这些数是有理数的平方.
(2)在上面例1中，$\sqrt {900}=30$，也就是$\sqrt {30^{2}}=30$。一般地，当$a≥0$时，$\sqrt {a^{2}}=a$成立吗？当$a\geqslant0$时,$\sqrt{a^{2}}=a$成立$a＜0$时，$\sqrt {a^{2}}=a$还成立吗？当$a＜0$时,$\sqrt{a^{2}}=a$不成立
(3)$(\sqrt {a})^{2}=a$成立吗？$(\sqrt{a})^{2}=a$成立这里的$a$是什么数？这里的a是非负数你是怎么理解的？与同伴进行交流。非负数算术平方根的平方等于本身

答案： 解:
(1)这些数是有理数的平方.
(2)当$a\geqslant0$时,$\sqrt{a^{2}}=a$成立;当$a＜0$时,$\sqrt{a^{2}}=a$不成立.
(3)$(\sqrt{a})^{2}=a$成立,这里的a是非负数,非负数算术平方根的平方等于本身.