《2025年精英新课堂九年级数学全一册北师大版贵州专版》

7. 如图，在两栋楼房之间的草坪中有一棵树，已知楼房AB的高度为10m，楼房CD的高度为15m，从A处看楼顶C处正好通过树顶E，而从D处看楼顶B处也正好通过树顶E. 求这棵树的高度.

答案： 7.解:
∵AB//CD,
∴∠B = ∠EDC,∠BAE = ∠C.
∴△ABE∽△CDE.
∴$\frac{BE}{DE}=\frac{AB}{CD}=\frac{2}{3}$.
∴$\frac{DE}{DB}=\frac{3}{5}$.
∵EF//AB,
∴∠DEF = ∠B.
∵∠EDF = ∠BDA,
∴△FDE∽△ADB.
∴$\frac{EF}{BA}=\frac{DE}{DB}=\frac{3}{5}$.
∴EF = $\frac{3}{5}$AB = 6m.答:这棵树的高度为6m.

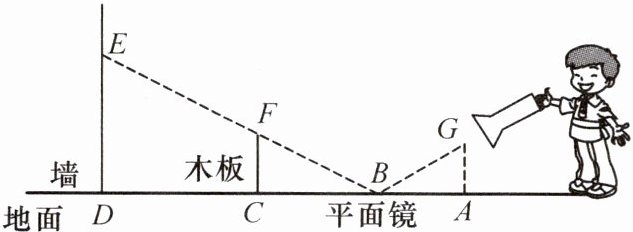
8. 如图，小明同学正在使用手电筒进行物理光学实验，地面上从左往右依次是墙、木板和平面镜. 手电筒的灯泡在点G处，手电筒的光从平面镜上点B处反射后，恰好经过木板的边缘点F，落在墙上的点E处，点E到地面的高度DE=3.5m，点F到地面的高度CF=1.5m，灯泡到木板的水平距离AC=5.4m，木板到墙的水平距离CD=4m. 已知光在镜面反射中的入射角等于反射角，图中点A，B，C，D在同一直线上.
（1）求BC的长；
（2）求灯泡到地面的高度AG.

答案： 8.解:
(1)由题意，得FC//DE,
∴∠BFC = ∠BED,∠BCF = ∠BDE.
∴△BFC∽△BED.
∴$\frac{BC}{BD}=\frac{FC}{DE}$，即$\frac{BC}{BC + 4}=\frac{1.5}{3.5}$.
∴BC = 3m.
(2)
∵AC = 5.4m,BC = 3m,
∴AB = AC - BC = 5.4 - 3 = 2.4(m).由题意,得∠FBC = ∠GBA,∠FCB = ∠GAB = 90°,
∴△BFC∽△BGA.
∴$\frac{AG}{CF}=\frac{AB}{BC}$，即$\frac{AG}{1.5}=\frac{2.4}{3}$.
∴AG = 1.2m.答:灯泡到地面的高度AG为1.2m.

9. 安顺白塔又叫望城塔，位于安顺的西秀山上，始建于元泰定三年（1326年），是安顺三大元代建筑之一. 小聪来游玩白塔后，很想知道白塔的高度，于是他用所学的知识进行测量求解，测量方法如下. 如图，先在点A处放一平面镜，小聪站在距A点1m的点B处，恰好在平面镜中看到塔的顶部点M. 再将平面镜沿NA方向移动3.6m至点D处（即AD=3.6m），小聪站在距D点1.6m的点E处，恰好再次在平面镜中看到塔的顶部点M. 已知小明眼睛到地面的距离CB=FE=1.7m，请根据题中提供的相关信息，求出白塔的高度MN.（平面镜大小忽略不计）

答案： 9.解:根据题意,得∠NAM = ∠BAC,∠ANM = ∠ABC = 90°,
∴△AMN∽△ACB.
∴$\frac{MN}{BC}=\frac{AN}{AB}$，即$\frac{MN}{1.7}=\frac{AN}{1}$.
∵∠NDM = ∠EDF,∠DNM = ∠DEF = 90°,
∴△MND∽△FED.
∴$\frac{MN}{EF}=\frac{DN}{DE}$，即$\frac{MN}{1.7}=\frac{3.6 + AN}{1.6}$.
∴$\frac{AN}{1}=\frac{3.6 + AN}{1.6}$.
∴AN = 6m.
∴$\frac{MN}{1.7}=\frac{6}{1}$.
∴MN = 10.2m.答:白塔的高度MN为10.2m.