《2025年精英新课堂九年级数学全一册北师大版贵州专版》

10.（2023·武汉中考）将$45^{\circ}$的$\angle AOB$按如图所示的方式放置在一把刻度尺上，顶点$O$与尺下沿的端点重合，$OA$与尺下沿重合，$OB$与尺上沿的交点$B$在尺上的读数为$2\ \text{cm}$. 若按相同的方式将$37^{\circ}$的$\angle AOC$放置在该刻度尺上，则$OC$与尺上沿的交点$C$在尺上的读数是______$\text{cm}$.（结果精确到$0.1\ \text{cm}$，参考数据：$\sin 37^{\circ} \approx 0.60$，$\cos 37^{\circ} \approx 0.80$，$\tan 37^{\circ} \approx 0.75$）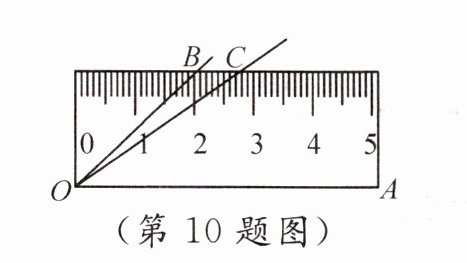

答案： 2.7

11. 如图，在$\triangle ABC$中，$AB = AC = 4$，$BC = 6$.
（1）求$\sin B$的值；
（2）延长$BC$至点$D$，使得$\angle ADB = 30^{\circ}$，求$CD$的长.

答案： 解：
(1)过点$A$作$AM\perp BC$于点$M$。$\because AB = AC$，$BC = 6$，$\therefore BM = CM=\frac{1}{2}BC = 3$。在$Rt\triangle ABM$中，$AM = \sqrt{AB^2 - BM^2}=\sqrt{7}$，$\therefore\sin B=\frac{AM}{AB}=\frac{\sqrt{7}}{4}$。
(2)在$Rt\triangle ADM$中，$\because\angle ADB = 30^{\circ}$，$\therefore DM=\frac{AM}{\tan\angle ADB}=\sqrt{21}$。$\therefore CD = DM - CM=\sqrt{21}-3$。

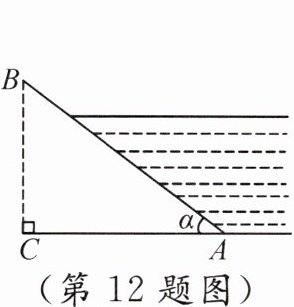
12. 如图，某水库堤坝横断面迎水坡的坡角为$\alpha$，$\sin\alpha = \frac{3}{5}$，堤坝高$BC = 30\ \text{m}$，则迎水坡面$AB$的长度为______$\text{m}$.

答案： 50

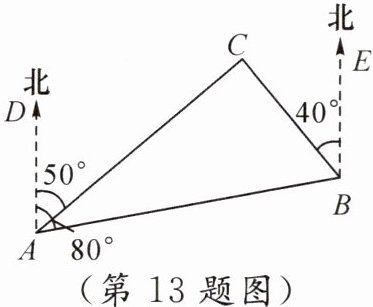
13.（2022·黔西南中考）如图，某海军舰艇在某海域$C$岛附近巡航，计划从$A$岛向北偏东$80^{\circ}$方向的$B$岛直线行驶. 测得$C$岛在$A$岛的北偏东$50^{\circ}$方向，在$B$岛的北偏西$40^{\circ}$方向. $A$，$B$之间的距离为$80\ \text{n mile}$，则$C$岛到航线$AB$的最短距离约是______$\text{n mile}$.（参考数据：$\sqrt{2} \approx 1.4$，$\sqrt{3} \approx 1.7$，结果保留整数）

答案： 34

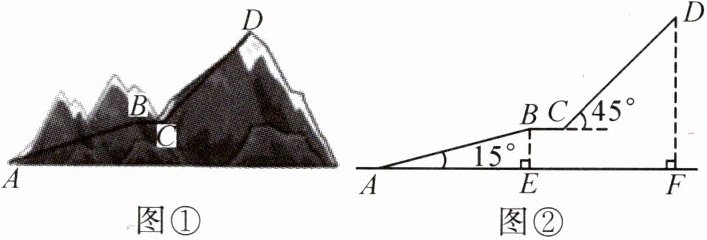
14.（2023·贵州中考）贵州旅游资源丰富. 某景区为给游客提供更好的游览体验，拟在如图①景区内修建观光索道. 设计示意图如图②所示，以山脚$A$为起点，沿途修建$AB$，$CD$两段长度相等的观光索道，最终到达山顶$D$处，中途设计了一段与$AF$平行的观光平台$BC$为$50\ \text{m}$. 索道$AB$与$AF$的夹角为$15^{\circ}$，$CD$与水平线夹角为$45^{\circ}$，$A$，$B$两处的水平距离$AE$为$576\ \text{m}$，$DF \perp AF$，垂足为$F$.（图中所有点都在同一平面内，点$A$，$E$，$F$在同一水平线上）
（1）求索道$AB$的长；
（2）求水平距离$AF$的长.
（结果精确到$1\ \text{m}$，参考数据：$\sin 15^{\circ} \approx 0.25$，$\cos 15^{\circ} \approx 0.96$，$\tan 15^{\circ} \approx 0.26$，$\sqrt{2} \approx 1.41$）

答案： 解：
(1)在$Rt\triangle ABE$中，$\angle AEB = 90^{\circ}$，$\angle A = 15^{\circ}$，$AE = 576\ m$，$\therefore AB=\frac{AE}{\cos A}=\frac{576}{\cos15^{\circ}}\approx600(m)$。答：索道$AB$的长约为$600\ m$。
(2)延长$BC$交$DF$于点$G$。$\because BC// AE$，$\therefore\angle CBE = 90^{\circ}$。$\because DF\perp AF$，$\therefore\angle AFD = 90^{\circ}$。$\because\angle BEF = 90^{\circ}$，$\therefore$四边形$BEFG$为矩形。$\therefore EF = BG$，$\angle CGD=\angle BGF = 90^{\circ}$。$\because CD = AB = 600\ m$，$\angle DCG = 45^{\circ}$，$\therefore CG = CD\cdot\cos\angle DCG = 300\sqrt{2}\ m$。$\therefore AF = AE + EF = AE + BG = AE + BC + CG = 576 + 50 + 300\sqrt{2}\approx1049(m)$，答：水平距离$AF$的长约为$1049\ m$。