《2025年精英新课堂九年级数学全一册北师大版贵州专版》

1. 已知关于$x$的一元二次方程$x^{2}+2x + a = 0$.
（1）若该方程有两个不相等的实数根，求$a$的取值范围；
（2）在（1）的条件下，该方程有一个实数根为$\sqrt{2}-1$，求方程的另一个根和$a$的值.@@解：(1)根据题意，得$\Delta = 2^{2}-4a＞0$，解得$a ＜ 1$。(2)设方程的另一个根为$t$。根据根与系数的关系，得$\sqrt{2}-1 + t=-2$，$(\sqrt{2}-1)t = a$，解得$t=-\sqrt{2}-1$，$a=-1$。$\therefore$方程的另一个根为$-\sqrt{2}-1$，$a$的值为$-1$。

答案： 1. 解：
(1)根据题意，得\(\Delta = 2^{2}-4a>0\)，解得\(a < 1\)。
(2)设方程的另一个根为\(t\)。根据根与系数的关系，得\(\sqrt{2}-1 + t=-2\)，\((\sqrt{2}-1)t = a\)，解得\(t=-\sqrt{2}-1\)，\(a=-1\)。\(\therefore\)方程的另一个根为\(-\sqrt{2}-1\)，\(a\)的值为\(-1\)。 

1.（六盘水期中）一个小球以15 m/s的初速度向上竖直弹出，它在空中的高度$h(\text{m})$与时间$t(\text{s})$满足关系式$h = 15t - 5t^{2}$. 当小球的高度为10 m时，$t$的值为（ ）
A. 1
B. 2
C. 1或2
D. 以上都不对

答案： C

2.【注重分类讨论思想】已知等腰三角形的一边长为4，另外两边长是关于$x$的方程$kx^{2}-(k + 8)x + 8 = 0$的两个根，求这个等腰三角形的周长.@@解：由题意，得$k\neq0$，$\Delta=[-(k + 8)]^{2}-4\times8k=(k - 8)^{2}\geqslant0$，$\therefore$无论$k$取任何非零实数，方程总有实数根。①当三角形的腰长为$4$时，设底边为$a$，$\therefore x = 4$是$kx^{2}-(k + 8)x + 8 = 0$的一根。$\therefore16k-4(k + 8)+8 = 0$，解得$k = 2$。由根与系数的关系，得$4a=\frac{8}{k}$，解得$a = 1$。此时$1 + 4＞4$，能够组成三角形，符合题意，此时周长为$4 + 4+1 = 9$；②当底边为$4$时，方程$kx^{2}-(k + 8)x + 8 = 0$有两个相等的实数根。$\therefore\Delta=(k - 8)^{2}=0$，解得$k_{1}=k_{2}=8$。$\therefore$原方程为$8x^{2}-16x + 8 = 0$，解得$x_{1}=x_{2}=1$。此时$1 + 1＜4$，不能组成三角形。综上所述，这个等腰三角形的周长为$9$。

答案： 2. 解：由题意，得\(k\neq0\)，\(\Delta=[-(k + 8)]^{2}-4\times8k=(k - 8)^{2}\geqslant0\)，\(\therefore\)无论\(k\)取任何非零实数，方程总有实数根。 ①当三角形的腰长为\(4\)时，设底边为\(a\)，\(\therefore x = 4\)是\(kx^{2}-(k + 8)x + 8 = 0\)的一根。\(\therefore16k-4(k + 8)+8 = 0\)，解得\(k = 2\)。由根与系数的关系，得\(4a=\frac{8}{k}\)，解得\(a = 1\)。此时\(1 + 4>4\)，能够组成三角形，符合题意，此时周长为\(4 + 4+1 = 9\)； ②当底边为\(4\)时，方程\(kx^{2}-(k + 8)x + 8 = 0\)有两个相等的实数根。\(\therefore\Delta=(k - 8)^{2}=0\)，解得\(k_{1}=k_{2}=8\)。\(\therefore\)原方程为\(8x^{2}-16x + 8 = 0\)，解得\(x_{1}=x_{2}=1\)。此时\(1 + 1<4\)，不能组成三角形。 综上所述，这个等腰三角形的周长为\(9\)。 

3. 已知$x_{1},x_{2}$是方程$4x^{2}-3x = 4x + 3$的两个实数根，不解方程，求下列代数式的值：
（1）$x_{1}x_{2}^{2}+x_{1}^{2}x_{2}$；
（2）$(x_{1}+3)(x_{2}+3)$；
（3）$\frac{x_{1}}{x_{2}}+\frac{x_{2}}{x_{1}}$.@@解：原方程化为一般形式为$4x^{2}-7x-3 = 0$。$\because x_{1}$，$x_{2}$是方程$4x^{2}-7x-3 = 0$的两个实数根，$\therefore x_{1}+x_{2}=\frac{7}{4}$，$x_{1}x_{2}=-\frac{3}{4}$。(1)$x_{1}x_{2}^{2}+x_{1}^{2}x_{2}=x_{1}x_{2}(x_{1}+x_{2})=(-\frac{3}{4})\times\frac{7}{4}=-\frac{21}{16}$。(2)$(x_{1}+3)(x_{2}+3)=x_{1}x_{2}+3(x_{1}+x_{2})+9=-\frac{3}{4}+3\times\frac{7}{4}+9=\frac{27}{2}$。(3)$\frac{x_{1}}{x_{2}}+\frac{x_{2}}{x_{1}}=\frac{x_{1}^{2}+x_{2}^{2}}{x_{1}x_{2}}=\frac{(x_{1}+x_{2})^{2}-2x_{1}x_{2}}{x_{1}x_{2}}=\frac{(\frac{7}{4})^{2}-2\times(-\frac{3}{4})}{-\frac{3}{4}}=-\frac{73}{12}$。

答案： 3. 解：原方程化为一般形式为\(4x^{2}-7x-3 = 0\)。\(\because x_{1}\)，\(x_{2}\)是方程\(4x^{2}-7x-3 = 0\)的两个实数根，\(\therefore x_{1}+x_{2}=\frac{7}{4}\)，\(x_{1}x_{2}=-\frac{3}{4}\)。
(1)\(x_{1}x_{2}^{2}+x_{1}^{2}x_{2}=x_{1}x_{2}(x_{1}+x_{2})=(-\frac{3}{4})\times\frac{7}{4}=-\frac{21}{16}\)。
(2)\((x_{1}+3)(x_{2}+3)=x_{1}x_{2}+3(x_{1}+x_{2})+9=-\frac{3}{4}+3\times\frac{7}{4}+9=\frac{27}{2}\)。
(3)\(\frac{x_{1}}{x_{2}}+\frac{x_{2}}{x_{1}}=\frac{x_{1}^{2}+x_{2}^{2}}{x_{1}x_{2}}=\frac{(x_{1}+x_{2})^{2}-2x_{1}x_{2}}{x_{1}x_{2}}=\frac{(\frac{7}{4})^{2}-2\times(-\frac{3}{4})}{-\frac{3}{4}}=-\frac{73}{12}\)。 

【变式题】与根的定义结合进行降次构造对称式
（1）已知$x_{1},x_{2}$为一元二次方程$2x^{2}+3x - 1 = 0$的两根，求$2x_{1}^{2}+4x_{1}+x_{2}$的值；（不解方程求解）
（2）已知$x_{1},x_{2}$为一元二次方程$x^{2}-3x + 1 = 0$的两根，求$2x_{1}^{2}+x_{2}^{2}-3x_{1}$的值.（不解方程求解）@@解：(1)$\because x_{1}$，$x_{2}$为一元二次方程$2x^{2}+3x - 1 = 0$的两根，$\therefore x_{1}+x_{2}=-\frac{3}{2}$，$2x_{1}^{2}+3x_{1}-1 = 0$，即$2x_{1}^{2}+3x_{1}=1$。$\therefore2x_{1}^{2}+4x_{1}+x_{2}=(2x_{1}^{2}+3x_{1})+(x_{1}+x_{2})=1-\frac{3}{2}=-\frac{1}{2}$。(2)$\because x_{1}$，$x_{2}$为一元二次方程$x^{2}-3x + 1 = 0$的两根，$\therefore x_{1}^{2}=3x_{1}-1$，$x_{2}^{2}=3x_{2}-1$，$x_{1}+x_{2}=3$。$\therefore2x_{1}^{2}+x_{2}^{2}-3x_{1}=2(3x_{1}-1)+(3x_{2}-1)-3x_{1}=3x_{1}+3x_{2}-3=3(x_{1}+x_{2})-3=3\times3 - 3 = 6$。

答案： 【变式题】解：
(1)\(\because x_{1}\)，\(x_{2}\)为一元二次方程\(2x^{2}+3x - 1 = 0\)的两根，\(\therefore x_{1}+x_{2}=-\frac{3}{2}\)，\(2x_{1}^{2}+3x_{1}-1 = 0\)，即\(2x_{1}^{2}+3x_{1}=1\)。\(\therefore2x_{1}^{2}+4x_{1}+x_{2}=(2x_{1}^{2}+3x_{1})+(x_{1}+x_{2})=1-\frac{3}{2}=-\frac{1}{2}\)。
(2)\(\because x_{1}\)，\(x_{2}\)为一元二次方程\(x^{2}-3x + 1 = 0\)的两根，\(\therefore x_{1}^{2}=3x_{1}-1\)，\(x_{2}^{2}=3x_{2}-1\)，\(x_{1}+x_{2}=3\)。\(\therefore2x_{1}^{2}+x_{2}^{2}-3x_{1}=2(3x_{1}-1)+(3x_{2}-1)-3x_{1}=3x_{1}+3x_{2}-3=3(x_{1}+x_{2})-3=3\times3 - 3 = 6\)。

4. 已知关于$x$的一元二次方程$x^{2}-6x+(2m + 1)=0$有实数根.
（1）求$m$的取值范围；
（2）如果方程的两个实数根为$x_{1},x_{2}$，且$2x_{1}x_{2}+x_{1}+x_{2}\geqslant20$，求$m$的取值范围.@@解：(1)根据题意，得$\Delta=(-6)^{2}-4(2m + 1)\geqslant0$，解得$m\leqslant4$。(2)根据题意，得$x_{1}+x_{2}=6$，$x_{1}x_{2}=2m + 1$。$\because2x_{1}x_{2}+x_{1}+x_{2}\geqslant20$，$\therefore2(2m + 1)+6\geqslant20$，解得$m\geqslant3$。$\because m\leqslant4$，$\therefore3\leqslant m\leqslant4$。

答案：  4. 解：
(1)根据题意，得\(\Delta=(-6)^{2}-4(2m + 1)\geqslant0\)，解得\(m\leqslant4\)。
(2)根据题意，得\(x_{1}+x_{2}=6\)，\(x_{1}x_{2}=2m + 1\)。\(\because2x_{1}x_{2}+x_{1}+x_{2}\geqslant20\)，\(\therefore2(2m + 1)+6\geqslant20\)，解得\(m\geqslant3\)。\(\because m\leqslant4\)，\(\therefore3\leqslant m\leqslant4\)。

5. 已知关于$x$的方程$x^{2}-4x + m + 2 = 0$有两个不相等的实数根.
（1）求$m$的取值范围；
（2）若$x_{1},x_{2}$是方程的两个根，是否存在实数$m$使得$x_{1}^{2}+x_{2}^{2}-x_{1}x_{2}=1$成立？若存在，请求出$m$的值；若不存在，请说明理由.@@解：(1)根据题意，得$\Delta=(-4)^{2}-4(m + 2)＞0$，解得$m＜2$。(2)不存在。理由如下：根据题意，得$x_{1}+x_{2}=4$，$x_{1}x_{2}=m + 2$。$\because x_{1}^{2}+x_{2}^{2}-x_{1}x_{2}=1$，$\therefore(x_{1}+x_{2})^{2}-3x_{1}x_{2}=1$，即$4^{2}-3(m + 2)=1$，解得$m = 3$。$\because m＜2$，$\therefore$不存在实数$m$使得$x_{1}^{2}+x_{2}^{2}-x_{1}x_{2}=1$成立。

答案：  5. 解：
(1)根据题意，得\(\Delta=(-4)^{2}-4(m + 2)>0\)，解得\(m<2\)。
(2)不存在。理由如下：根据题意，得\(x_{1}+x_{2}=4\)，\(x_{1}x_{2}=m + 2\)。\(\because x_{1}^{2}+x_{2}^{2}-x_{1}x_{2}=1\)，\(\therefore(x_{1}+x_{2})^{2}-3x_{1}x_{2}=1\)，即\(4^{2}-3(m + 2)=1\)，解得\(m = 3\)。\(\because m<2\)，\(\therefore\)不存在实数\(m\)使得\(x_{1}^{2}+x_{2}^{2}-x_{1}x_{2}=1\)成立。 

6. 已知关于$x$的一元二次方程$x^{2}-4x - 2m + 5 = 0$有两个不相等的实数根.
（1）求实数$m$的取值范围；
（2）若该方程的两个根都是符号相同的实数，当$m$是最小整数时，试求该方程的根.@@解：(1)根据题意，得$\Delta=(-4)^{2}-4(-2m + 5)＞0$，解得$m＞\frac{1}{2}$。(2)设$x_{1}$，$x_{2}$是方程的两根。根据题意，得$x_{1}+x_{2}=4＞0$，$x_{1}x_{2}=-2m + 5＞0$，解得$m＜\frac{5}{2}$。$\because m＞\frac{1}{2}$，$\therefore\frac{1}{2}＜m＜\frac{5}{2}$。$\because m$是最小整数，$\therefore m = 1$。当$m = 1$时，原方程是$x^{2}-4x + 3 = 0$，解得$x_{1}=1$，$x_{2}=3$。

答案： 解：
(1)根据题意，得$\Delta=(-4)^{2}-4(-2m + 5)＞0$，解得$m＞\frac{1}{2}$。
(2)设$x_{1}$，$x_{2}$是方程的两根。根据题意，得$x_{1}+x_{2}=4＞0$，$x_{1}x_{2}=-2m + 5＞0$，解得$m＜\frac{5}{2}$。$\because m＞\frac{1}{2}$，$\therefore\frac{1}{2}＜m＜\frac{5}{2}$。$\because m$是最小整数，$\therefore m = 1$。当$m = 1$时，原方程是$x^{2}-4x + 3 = 0$，解得$x_{1}=1$，$x_{2}=3$。

7. 已知$x_{1},x_{2}$是关于$x$的方程$x^{2}+mx - m = 0$的两个实数根，$x_{1},x_{2}$满足$(x_{1}-x_{2})^{2}=5$，且$x_{1}x_{2}＜0$.
（1）求$m$的值；
（2）不解方程求$3x_{1}-x_{2}^{2}$的值.@@解：(1)$\because x_{1}$，$x_{2}$是关于$x$的方程$x^{2}+mx - m = 0$的两个实数根，$\therefore x_{1}+x_{2}=-m$，$x_{1}x_{2}=-m$。$\therefore(x_{1}-x_{2})^{2}=(x_{1}+x_{2})^{2}-4x_{1}x_{2}=m^{2}+4m = 5$，解得$m_{1}=1$，$m_{2}=-5$。$\because x_{1}x_{2}＜0$，$\therefore - m＜0$，解得$m＞0$。$\therefore m = 1$。(2)当$m = 1$时，原方程为$x^{2}+x - 1 = 0$，$\therefore x_{1}+x_{2}=-1$，$x_{1}x_{2}=-1$，$x_{1}^{2}=1 - x_{1}$，$x_{2}^{2}=1 - x_{2}$。$\therefore3x_{1}-x_{2}^{4}=3x_{1}-(1 - x_{2})^{2}=3x_{1}-1 + 2x_{2}-x_{2}^{2}=3x_{1}-1 + 2x_{2}-(1 - x_{2})=3(x_{1}+x_{2})-2=-3 - 2=-5$。

答案：
(1)$\because x_{1}$，$x_{2}$是关于$x$的方程$x^{2}+mx - m = 0$的两个实数根，$\therefore x_{1}+x_{2}=-m$，$x_{1}x_{2}=-m$。$\therefore(x_{1}-x_{2})^{2}=(x_{1}+x_{2})^{2}-4x_{1}x_{2}=m^{2}+4m = 5$，解得$m_{1}=1$，$m_{2}=-5$。$\because x_{1}x_{2}＜0$，$\therefore - m＜0$，解得$m＞0$。$\therefore m = 1$。
(2)当$m = 1$时，原方程为$x^{2}+x - 1 = 0$，$\therefore x_{1}+x_{2}=-1$，$x_{1}x_{2}=-1$，$x_{1}^{2}=1 - x_{1}$，$x_{2}^{2}=1 - x_{2}$。$\therefore3x_{1}-x_{2}^{4}=3x_{1}-(1 - x_{2})^{2}=3x_{1}-1 + 2x_{2}-x_{2}^{2}=3x_{1}-1 + 2x_{2}-(1 - x_{2})=3(x_{1}+x_{2})-2=-3 - 2=-5$。

答案：

2. 某赛车在一段时间内行驶的路程$s(\text{m})$和时间$t(\text{s})$之间的关系为$s = 4t^{2}+10t$，则在这段时间内该赛车行驶300 m需要______s.

答案： 7.5

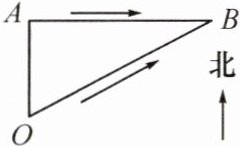
3. 如图，某海关缉私艇在点$O$处发现在正北方向30 n mile的$A$处有一艘可疑船只，测得它正以60 n mile/h的速度向正东方向航行，随即调整方向，以75 n mile/h的速度准备在$B$处拦截. 问经过多少时间能赶上？

答案： 解:设经过$x$ h能赶上. 由题意，得$\angle A = 90^{\circ}$，$\therefore OB^{2}=OA^{2}+AB^{2}$，即$(75x)^{2}=30^{2}+(60x)^{2}$，解得$x_{1}=\frac{2}{3}$，$x_{2}=-\frac{2}{3}$（不合题意，舍去）. 答:经过$\frac{2}{3}$ h能赶上.

4.（教材P53习题T3变式）有一个面积为16 cm²的梯形，它的一条底边长为3 cm，另一条底边比它的高长1 cm. 若设这条底边长为$x$ cm，根据题意，列出方程整理后为（ ）
A. $x^{2}+2x - 35 = 0$
B. $x^{2}+2x - 70 = 0$
C. $x^{2}-2x - 35 = 0$
D. $x^{2}-2x + 70 = 0$

答案： A

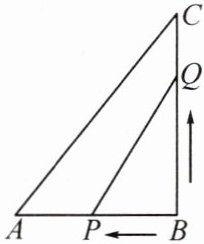
5.（教材P53习题T2变式）如图，在Rt△ABC中，∠B = 90°，AB = 4 cm，BC = 5 cm，点$P$从点$B$出发，沿$BA$以1 cm/s的速度向点$A$运动，同时，点$Q$从点$B$出发，沿$BC$以2 cm/s的速度向点$C$运动. 问点$P$，$Q$出发几秒后，可使△PQB的面积为四边形ACQP面积的$\frac{2}{3}$？

答案： 解:由题意，得$S_{\triangle ABC}=\frac{1}{2}\times4\times5 = 10$，$S_{\triangle PBQ}=\frac{2}{5}S_{\triangle ABC}$. 设运动时间为$t$ s，则$BP = t$ cm，$BQ = 2t$ cm. $\therefore\frac{1}{2}t\cdot2t = 10\times\frac{2}{5}$，解得$t_{1}=-2$（舍去），$t_{2}=2$. 当$t = 2$时，$BP = 2$ cm$＜4$ cm，$BQ = 2t = 4$ cm$＜5$ cm，符合题意. 答:点$P$，$Q$出发$2$ s后，可使$\triangle PQB$的面积为四边形$ACQP$面积的$\frac{2}{3}$.

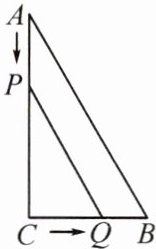
6.（教材P54习题T4变式）如图，在△ABC中，∠C = 90°，BC = 5 cm，AB = 5$\sqrt{5}$ cm，点$P$从点$A$出发，沿边$AC$以2 cm/s的速度向终点$C$匀速移动，同时，点$Q$从点$C$出发，沿边$CB$以1 cm/s的速度向终点$B$匀速移动. 运动几秒时，$P$，$Q$两点间的距离是2$\sqrt{10}$ cm？

答案： 解:设运动$x$ s时，$P$，$Q$两点间的距离是$2\sqrt{10}$ cm，则$AP = 2x$ cm，$CQ = x$ cm. 在$\triangle ABC$中，$\angle C = 90^{\circ}$，$BC = 5$ cm，$AB = 5\sqrt{5}$ cm，$\therefore AC=\sqrt{AB^{2}-BC^{2}} = 10$ cm. $\therefore CP=(10 - 2x)$ cm. 在$Rt\triangle CPQ$中，$PC^{2}+CQ^{2}=PQ^{2}$，$\therefore(10 - 2x)^{2}+x^{2}=(2\sqrt{10})^{2}$，解得$x = 2$或$x = 6$. 当$x = 6$时$CP = 10 - 2x=-2＜0$，$\therefore x = 6$不合题意舍去. $\therefore$运动$2$ s时，$P$，$Q$两点间的距离是$2\sqrt{10}$ cm.