《2025年精英新课堂九年级数学全一册北师大版贵州专版》

6.某企业投入60万元(只计入第一年成本)生产某种产品，按网上订单生产并销售(生产量等于销售量).经测算，该产品网上每年的销售量y(万件)与售价x(元/件)之间满足函数关系式y = 24 - x，第一年除60万元外，其他成本为8元/件.
(1)求该产品第一年的利润w(万元)与售价x之间的函数关系式;
(2)该产品第一年的利润为4万元，第二年将它全部作为技改资金再次投入(只计入第二年成本)后，其他成本下降2元/件.
①求该产品第一年的售价;
②若第二年的售价不高于第一年，销售量不超过13万件，则第二年的利润最少是多少万元？

答案： 解：
(1)根据题意，得$w=(x - 8)(24 - x)-60=-x^{2}+32x - 252$.
(2)①$\because$该产品第一年的利润为4万元，$\therefore4=-x^{2}+32x - 252$，解得$x_{1}=x_{2}=16$.$\therefore$该产品第一年的售价是16元/件. ②根据题意，得$\begin{cases}x\leqslant16\\24 - x\leqslant13\end{cases}$，解得$11\leqslant x\leqslant16$. 设第二年的利润是$w'$万元. 根据题意，得$w'=(x - 8 + 2)(24 - x)-4=-(x - 15)^{2}+77(11\leqslant x\leqslant16)$，$\therefore$当$x = 11$时，$w'$有最小值，最小值为$-4^{2}+77 = 61$. 答：第二年的利润最少是61万元.

7.(2023.临沂中考)综合与实践:
问题情境:
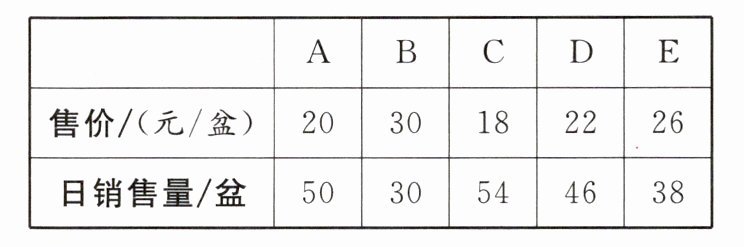
小莹妈妈的花卉超市以15元/盆的价格新购进了某种盆栽，为了确定售价，小莹帮妈妈调查了附近A,B,C,D,E五家花卉店近期该种盆栽的售价与日销售量情况，记录如下:

数据整理:
(1)请将以上调查数据按照一定顺序重新整理,填写在下表中;

模型建立:
(2)分析数据的变化规律，找出日销售量与售价间的关系;
拓广应用:
(3)由以上信息，小莹妈妈在销售该种花卉中，
①要想每天获得400元，应如何定价？
②当售价为多少时，每天获得的利润最大？

答案： 解：
(1)18 54 20 50 22 46 26 38 30 30
(2)观察表格可知销售量是售价的一次函数. 设日销售量为$y$盆，售价为$x$元/盆，$y$关于$x$的函数表达式为$y = kx + b$. 把$(18,54)$，$(20,50)$代入，得$\begin{cases}18k + b = 54\\20k + b = 50\end{cases}$，解得$\begin{cases}k = -2\\b = 90\end{cases}$.$\therefore y=-2x + 90$.
(3)①根据题意，得$(x - 15)(-2x + 90)=400$，解得$x_{1}=25$，$x_{2}=35$.$\therefore$要想每天获得400元，定价应为25元/盆或35元/盆. ②设每天获得的利润为$w$元. 根据题意，得$w=(x - 15)(-2x + 90)=-2x^{2}+120x - 1350=-2(x - 30)^{2}+450$.$\because -2\lt0$，$\therefore$当$x = 30$时，$w$取最大值，最大值为450.$\therefore$当售价定为30元时，每天能够获得最大利润450元.