2025年精英新课堂九年级数学全一册北师大版贵州专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年精英新课堂九年级数学全一册北师大版贵州专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第100页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
8.已知蓄电池的电压为定值,使用蓄电池时,电流I(A)与电阻R(Ω)是反比例函数关系,它的图象如图所示,下列说法正确的是( )
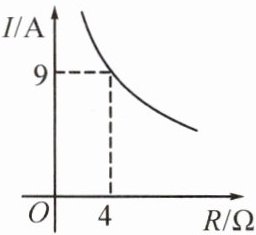
A.函数表达式为I=$\frac{13}{R}$
B.蓄电池的电压是18V
C.当I≤10A时,R≥3.6Ω
D.当R=6Ω时,I=4A

A.函数表达式为I=$\frac{13}{R}$
B.蓄电池的电压是18V
C.当I≤10A时,R≥3.6Ω
D.当R=6Ω时,I=4A
答案:
C
9.验光师通过检测发现,近视眼镜的度数y(度)与镜片焦距x(m)成反比例,y关于x的函数图象如图所示.经过一段时间的矫正治疗后,小雪的镜片焦距由0.25m调整到0.5m,则近视眼镜的度数减少了______度.
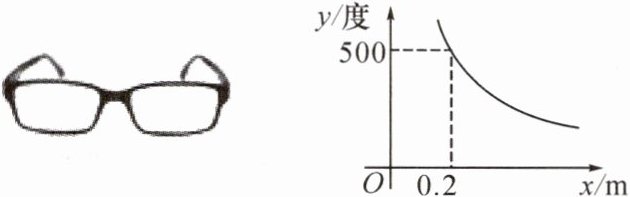

答案:
200
10.(2023.常德中考)如图,一次函数y=−x+m与反比例函数y=$\frac{k}{x}$的图象相交于点A和点B(3,−1).
(1)求m的值和反比例函数的表达式;
(2)当−x+m>$\frac{k}{x}$时,求x的取值范围.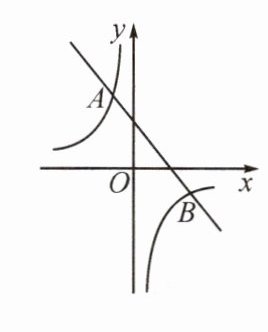
(1)求m的值和反比例函数的表达式;
(2)当−x+m>$\frac{k}{x}$时,求x的取值范围.

答案:
解:
(1)把$B(3, - 1)$分别代入$y=-x + m$,$y=\frac{k}{x}$,得$-1=-3 + m$,$-1=\frac{k}{3}$,解得$m = 2$,$k=-3$.$\therefore$反比例函数的表达式为$y=-\frac{3}{x}$.
(2)由
(1),得一次函数的表达式为$y=-x + 2$.联立$\begin{cases}y=-x + 2\\y=-\frac{3}{x}\end{cases}$,解得$\begin{cases}x=-1\\y = 3\end{cases}$或$\begin{cases}x = 3\\y=-1\end{cases}$.$\therefore$点$A$的坐标为$(-1,3)$.观察图象可得,当$-x + m>\frac{k}{x}$时,$x$的取值范围是$x<-1$或$0<x<3$.
(1)把$B(3, - 1)$分别代入$y=-x + m$,$y=\frac{k}{x}$,得$-1=-3 + m$,$-1=\frac{k}{3}$,解得$m = 2$,$k=-3$.$\therefore$反比例函数的表达式为$y=-\frac{3}{x}$.
(2)由
(1),得一次函数的表达式为$y=-x + 2$.联立$\begin{cases}y=-x + 2\\y=-\frac{3}{x}\end{cases}$,解得$\begin{cases}x=-1\\y = 3\end{cases}$或$\begin{cases}x = 3\\y=-1\end{cases}$.$\therefore$点$A$的坐标为$(-1,3)$.观察图象可得,当$-x + m>\frac{k}{x}$时,$x$的取值范围是$x<-1$或$0<x<3$.
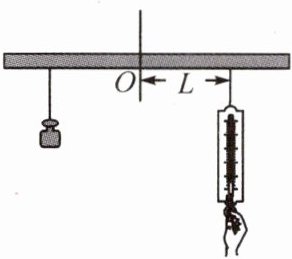
11.[注重实践探究]如图,取一根长1m的质地均匀的木杆,用细绳绑在木杆的中点O处,并将其吊起来,在中点O的左侧且距离中点30cm处挂一个重9.8N的物体,同时在中点O的右侧用一个弹簧秤向下拉,使木杆保持平衡,改变弹簧秤与中点O的距离L(单位:cm),看弹簧秤的示数F(单位:N,精确到0.1N)有什么变化.小慧在做此数学活动时,得到下表的数据:
结果老师发现其中有一组数据明显有错误.
(1)当L=________cm时所对应的F的数据是明显错误的;
(2)在已学过的函数中选择合适的模型求出F与L之间的函数关系式;
(3)若弹簧秤的最大量程是60N,求L的取值范围.
结果老师发现其中有一组数据明显有错误.
(1)当L=________cm时所对应的F的数据是明显错误的;
(2)在已学过的函数中选择合适的模型求出F与L之间的函数关系式;
(3)若弹簧秤的最大量程是60N,求L的取值范围.

答案:
解:
(1)10
(2)根据杠杆原理知$F\cdot L=30\times9.8 = 294$,$\therefore F$与$L$之间的函数关系式为$F=\frac{294}{L}$.
(3)当$F = 60\ N$时,$\frac{294}{L}=60$,解得$L = 4.9$.根据反比例函数的图象与性质可得,当$F\leqslant60$时,$L\geqslant4.9$.由题意可知$L\leqslant50$,$\therefore L$的取值范围是$4.9\ cm\leqslant L\leqslant50\ cm$.
(1)10
(2)根据杠杆原理知$F\cdot L=30\times9.8 = 294$,$\therefore F$与$L$之间的函数关系式为$F=\frac{294}{L}$.
(3)当$F = 60\ N$时,$\frac{294}{L}=60$,解得$L = 4.9$.根据反比例函数的图象与性质可得,当$F\leqslant60$时,$L\geqslant4.9$.由题意可知$L\leqslant50$,$\therefore L$的取值范围是$4.9\ cm\leqslant L\leqslant50\ cm$.
查看更多完整答案,请扫码查看


