《2025年精英新课堂九年级数学全一册北师大版贵州专版》

9. 下列一元二次方程中，没有实数根的是（ ）
A. $9x^{2} + 6x + 1 = 0$
B. $x^{2} - 2x - 3 = 0$
C. $7x^{2} + 2x + 3 = 0$
D. $2x^{2} + x - 1 = 0$

答案： C

10.（2023·聊城中考）若关于$x$的一元二次方程$mx^{2} + 2x + 1 = 0$有实数根，则$m$的取值范围是（ ）
A. $m \geq -1$
B. $m \leq 1$
C. $m \geq -1$且$m \neq 0$
D. $m \leq 1$且$m \neq 0$

答案： D

11.（2023·兰州中考）若关于$x$的一元二次方程$x^{2} + bx + c = 0$有两个相等的实数根，则$b^{2} - 2(1 + 2c)$的值为（ ）
A. -2
B. 2
C. -4
D. 4

答案： A

12.（2023·眉山中考）若方程$x^{2} - 3x - 4 = 0$的根为$x_{1}$，$x_{2}$，则$(x_{1} + 2)(x_{2} + 2)$的值为____。

答案： 6

13.（2023·襄阳中考）关于$x$的一元二次方程$x^{2} + 2x + 3 - k = 0$有两个不相等的实数根。
（1）求$k$的取值范围；
（2）若方程的两个根为$\alpha$，$\beta$，且$k^{2} = \alpha\beta + 3k$，求$k$的值。

答案： 解：
(1)$b^2 - 4ac = 2^2 - 4\times1\times(3 - k) = -8 + 4k$. $\because$该方程有两个不相等的实数根，$\therefore -8 + 4k＞0$，解得$k＞2$.
(2)$\because$方程的两个根为$\alpha,\beta$，$\therefore\alpha\beta = 3 - k$. $\therefore k^2 = 3 - k + 3k$，解得$k_1 = 3,k_2 = -1$. 由
(1)知$k＞2$，$\therefore k$的值为 3.

14.（2023 - 2024·贵阳期中）生物兴趣小组的同学将自己收集的标本向本组其他成员各赠送一件，全组共相互赠送标本210件。设全组有$x$名同学，则根据题意列出方程是（ ）
A. $x(x + 1) = 210$
B. $x(x - 1) = 210$
C. $2x(x + 1) = 210$
D. $\frac{1}{2}x(x - 1) = 210$

答案： B

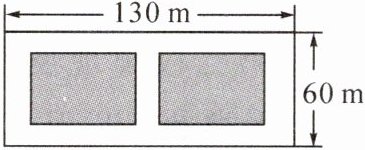
15. 如图，某农家乐老板计划在一块长130 m，宽60 m的空地上挖两块形状大小相同的垂钓鱼塘，它们的面积之和为5750 m²。若在两块垂钓鱼塘之间及周边留有宽度相等的垂钓通道，则垂钓通道的宽度为____m。

答案： 5

16.（2023 - 2024·安顺关岭县期末）某水果商经销一种水果，原价为每千克50元，连续两次降价后每千克32元，已知每次下降的百分率相同。
（1）求每次下降的百分率；
（2）若每千克盈利10元，则每天可售出500 kg。经市场调查发现，在进货价不变的情况下，水果商决定采取适当的涨价措施，若每千克涨价1元，则日销售量将减少20 kg。现该水果商要保证每天盈利6000元，且要尽快减少库存，那么每千克应涨价多少元？

答案： 解：
(1) 设每次下降的百分率为$a$. 根据题意，得$50(1 - a)^2 = 32$，解得$a = 1.8$（舍去）或$a = 0.2 = 20\%$. 答：每次下降的百分率为 20%.
(2) 设每千克应涨价$x$元. 根据题意，得$(10 + x)(500 - 20x) = 6000$. 解得$x_1 = 5,x_2 = 10$. $\because$要尽快减少库存，$\therefore x = 5$. 答：每千克应涨价 5 元.