第54页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
问题导入 [教材第45页例题]
啤酒厂要生产一批啤酒,每天生产的吨数与需要的天数如下表。

每天生产的吨数和需要的天数这两种量有什么关系呢?
1. 理解题意:通过观察统计表,找到表中相关联的两种量,观察两种量的变化规律,认识这两种量的关系。
2. 观察统计表。
(1)表格中有两种量,分别是每天生产的吨数和需要的天数。
(2)观察表中数据,发现需要的天数随着每天生产的吨数的变化而变化。
(3)从左往右看表中数据,发现每天生产的吨数越多,需要的天数就越少;从右往左看表中数据,发现每天生产的吨数越少,需要的天数就越多,它们是相关联的量。
3. 计算并比较两种量相对应的两个数的积。
100×60 = 6000
200×30 = 6000
300×20 = 6000
400×15 = 6000
500×12 = 6000
……
我发现:每天生产的吨数和需要的天数的积一定。
每天生产的吨数和需要的天数的积就是生产啤酒的总吨数,生产的这批啤酒的总吨数是不变的。
4. 认识反比例的意义。
通过计算发现:无论每天生产的吨数和需要的天数怎样变化,生产的总吨数不变。用式子表示它们的关系:每天生产的吨数×需要的天数 = 总吨数(一定)。
小提示
判断两种量是否成反比例的关键是这两种量中相对应的两个数的乘积是否一定。
像这样,每天生产的吨数变化,需要的天数也随着变化,总吨数不变,也就是每天生产的吨数与需要的天数的积一定,我们就说每天生产的吨数和需要的天数是成反比例的量,它们的关系叫作反比例关系。
5. 反比例关系的字母表达式。
如果用字母x和y分别表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用式子表示为x×y = k(一定)。
6. 反比例关系的判断方法。
(1)确定这两种量是相关联的量。
(2)看这两种量中相对应的两个数的积是否一定,若积一定,这两种量就成反比例关系,否则,就不成反比例关系。
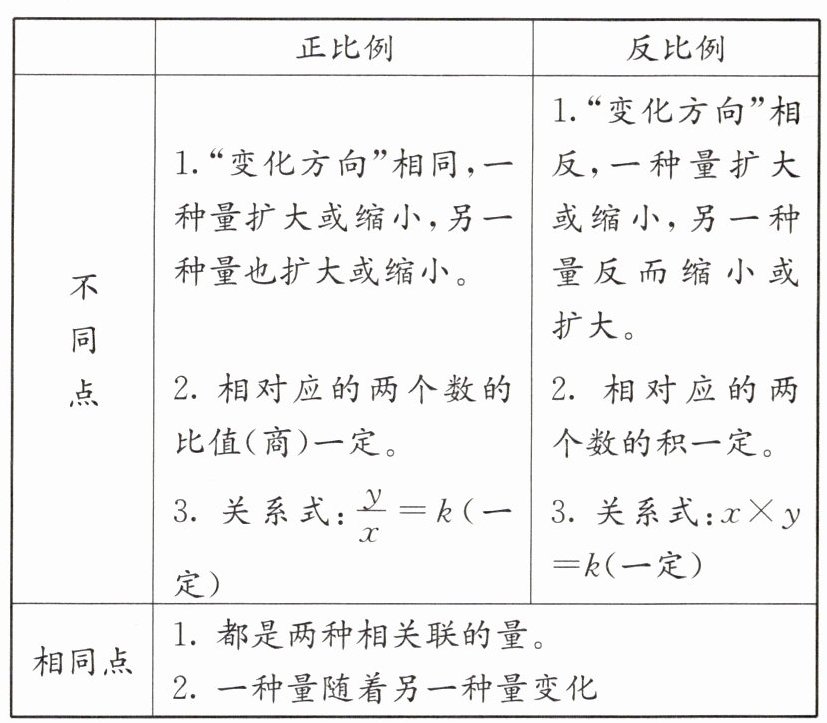
7. 拓展探究:正比例与反比例的异同点如下表。
归纳总结
1. 两种相关联的量,一种量变化,另一种量也随着变化。如果这两种量中相对应的两个数的积一定,这两种量就叫作成反比例的量,它们的关系叫作反比例关系。
2. 如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以表示为x×y = k(一定)。
3. 判断两种量是否成反比例的方法:①确定这两种量是相关联的量。②看这两种量中相对应的两个数的积是否一定,若积一定,这两种量就成反比例关系,否则,就不成反比例关系。
啤酒厂要生产一批啤酒,每天生产的吨数与需要的天数如下表。

每天生产的吨数和需要的天数这两种量有什么关系呢?
1. 理解题意:通过观察统计表,找到表中相关联的两种量,观察两种量的变化规律,认识这两种量的关系。
2. 观察统计表。
(1)表格中有两种量,分别是每天生产的吨数和需要的天数。
(2)观察表中数据,发现需要的天数随着每天生产的吨数的变化而变化。
(3)从左往右看表中数据,发现每天生产的吨数越多,需要的天数就越少;从右往左看表中数据,发现每天生产的吨数越少,需要的天数就越多,它们是相关联的量。
3. 计算并比较两种量相对应的两个数的积。
100×60 = 6000
200×30 = 6000
300×20 = 6000
400×15 = 6000
500×12 = 6000
……
我发现:每天生产的吨数和需要的天数的积一定。
每天生产的吨数和需要的天数的积就是生产啤酒的总吨数,生产的这批啤酒的总吨数是不变的。
4. 认识反比例的意义。
通过计算发现:无论每天生产的吨数和需要的天数怎样变化,生产的总吨数不变。用式子表示它们的关系:每天生产的吨数×需要的天数 = 总吨数(一定)。
小提示
判断两种量是否成反比例的关键是这两种量中相对应的两个数的乘积是否一定。
像这样,每天生产的吨数变化,需要的天数也随着变化,总吨数不变,也就是每天生产的吨数与需要的天数的积一定,我们就说每天生产的吨数和需要的天数是成反比例的量,它们的关系叫作反比例关系。
5. 反比例关系的字母表达式。
如果用字母x和y分别表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用式子表示为x×y = k(一定)。
6. 反比例关系的判断方法。
(1)确定这两种量是相关联的量。
(2)看这两种量中相对应的两个数的积是否一定,若积一定,这两种量就成反比例关系,否则,就不成反比例关系。
7. 拓展探究:正比例与反比例的异同点如下表。

归纳总结
1. 两种相关联的量,一种量变化,另一种量也随着变化。如果这两种量中相对应的两个数的积一定,这两种量就叫作成反比例的量,它们的关系叫作反比例关系。
2. 如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以表示为x×y = k(一定)。
3. 判断两种量是否成反比例的方法:①确定这两种量是相关联的量。②看这两种量中相对应的两个数的积是否一定,若积一定,这两种量就成反比例关系,否则,就不成反比例关系。
答案:
查看更多完整答案,请扫码查看


