第35页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
问题导入[教材第25页例题]

圆锥形包装盒的体积是多少立方厘米?(如上图)
1.理解题意:求包装盒的体积就是求底面直径是6cm,高是10cm的圆锥的体积。
2.探究圆锥体积的计算公式。
(1)探究圆锥和圆柱体积之间的关系。
①实验准备:准备好等底等高的圆柱形、圆锥形透明容器及一些加色的水。
②实验过程:
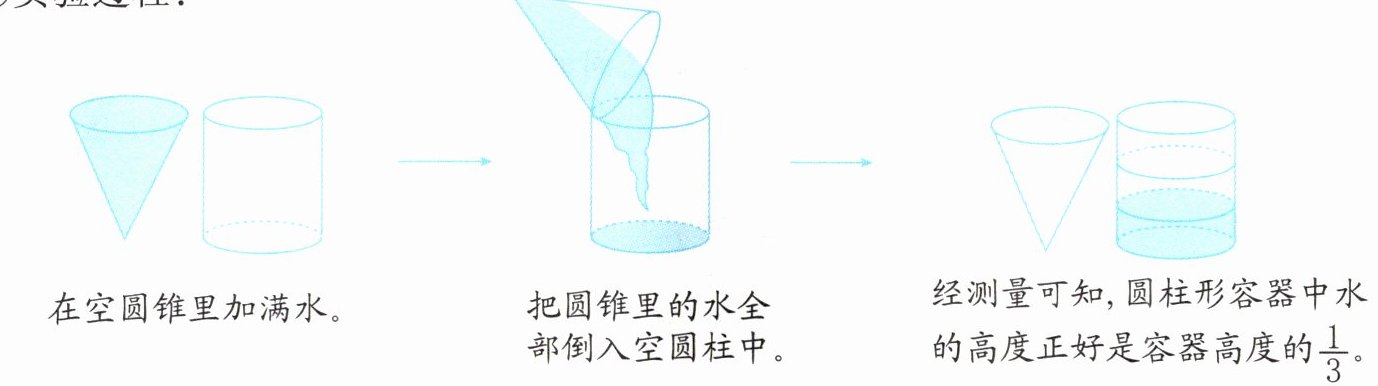
③实验结论:圆锥的体积等于和它等底等高的圆柱体积的三分之一。
(2)推导公式:因为圆柱的体积=底面积×高,与圆柱等底等高的圆锥的体积等于该圆柱体积的$\frac{1}{3}$,所以圆锥的体积=$\frac{1}{3}$×底面积×高,字母公式为V=$\frac{1}{3}$Sh。
3.解决问题。
底面积:3.14×(6÷2)²=28.26(cm²) 体积:28.26×10×$\frac{1}{3}$=94.2(cm³)
答:圆锥形包装盒的体积是94.2cm³。
4.拓展探究:一个圆柱和一个圆锥,底面积、高和体积其中任意两个量相等时,另一个量都是3倍的关系:底面积和体积相等,3×圆柱的高=圆锥的高;高和体积相等,3×圆柱的底面积=圆锥的底面积;底面积和高相等,3×圆锥的体积=圆柱的体积。
归纳总结
圆锥的体积公式:圆锥的体积=$\frac{1}{3}$×底面积×高,字母公式为V=$\frac{1}{3}$Sh。

圆锥形包装盒的体积是多少立方厘米?(如上图)
1.理解题意:求包装盒的体积就是求底面直径是6cm,高是10cm的圆锥的体积。
2.探究圆锥体积的计算公式。
(1)探究圆锥和圆柱体积之间的关系。
①实验准备:准备好等底等高的圆柱形、圆锥形透明容器及一些加色的水。

②实验过程:

③实验结论:圆锥的体积等于和它等底等高的圆柱体积的三分之一。
(2)推导公式:因为圆柱的体积=底面积×高,与圆柱等底等高的圆锥的体积等于该圆柱体积的$\frac{1}{3}$,所以圆锥的体积=$\frac{1}{3}$×底面积×高,字母公式为V=$\frac{1}{3}$Sh。
3.解决问题。
底面积:3.14×(6÷2)²=28.26(cm²) 体积:28.26×10×$\frac{1}{3}$=94.2(cm³)
答:圆锥形包装盒的体积是94.2cm³。
4.拓展探究:一个圆柱和一个圆锥,底面积、高和体积其中任意两个量相等时,另一个量都是3倍的关系:底面积和体积相等,3×圆柱的高=圆锥的高;高和体积相等,3×圆柱的底面积=圆锥的底面积;底面积和高相等,3×圆锥的体积=圆柱的体积。
归纳总结
圆锥的体积公式:圆锥的体积=$\frac{1}{3}$×底面积×高,字母公式为V=$\frac{1}{3}$Sh。
答案:
查看更多完整答案,请扫码查看


