《2026年山东省中考试卷精选九年级数学》

6. 如图，在$ Rt \triangle ABC$ 中，$AC = 4$，$BC = 3$，D 为 AC 的中点，过点 D 作$DE \perp AB$，交 AB 于点 E，则 DE 的长为 (A).


A.$\frac{6}{5}$
B.$\frac{4}{3}$
C.2
D.$2\sqrt{3}$

答案： 6.A [解析]本题考查了相似三角形的判定和性质、勾股定理.在$ Rt \triangle ABC$中,$AC = 4$,$BC = 3$,由勾股定理可得$AB = \sqrt{3^2 + 4^2} = 5$.$\because D$为$AB$的中点,$DE \perp AB$,交$AC$于点$E$,$\therefore AD = \frac{1}{2} AC = 2$,$\angle AED = \angle C = 90°$.$\because \angle EAD = \angle CAB$,$\therefore \triangle EAD \sim \triangle CAB$,$\therefore \frac{AD}{AB} = \frac{DE}{BC}$,即$\frac{2}{5} = \frac{DE}{3}$,解得$DE = \frac{6}{5}$.故选A.

7. 一个不透明的袋子中装有 4 个分别标有化学元素符号 H，O，C，N 的小球，这些小球除元素符号外无其他差别，从袋子中随机摸出两个小球，所标元素能组成“CO”(一氧化碳)的概率是 (D).

A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{1}{4}$
D.$\frac{1}{6}$

答案：
7.D [解析]本题考查了画树状图求概率.依题意画树状图如图,由图可知共有12种等可能的结果,其中所标元素能组成“$CO$”(一氧化碳)的结果数为2,所以从袋子中随机摸出两个小球,所标元素能组成“$CO$”(一氧化碳)的概率$= \frac{2}{12} = \frac{1}{6}$.故选D.

8. 如图，一名男生推铅球，铅球行进高度 y(单位：m)与水平距离 x(单位：m)之间的关系式为$y = -\frac{1}{12}x^{2} + \frac{2}{3}x + \frac{5}{3}$，有下列结论：①该男生推铅球出手时，铅球的高度为$\frac{5}{3}$m；②铅球飞行至水平距离 4 m 时，达到最大高度，最大高度为 3 m；③铅球落地时的水平距离为 10 m.其中，正确结论的个数是 (D).

A.0
B.1
C.2
D.3

答案： 8.D [解析]本题考查了二次函数的实际应用.$\because y = - \frac{1}{12} x^2 + \frac{2}{3} x + \frac{5}{3}$,$\therefore$当$x = 0$时,$y = \frac{5}{3}$,故①正确;$\because y = - \frac{1}{12} x^2 + \frac{2}{3} x + \frac{5}{3} = - \frac{1}{12} (x - 4)^2 + 3$,$\therefore$当$x = 4$时,$y$有最大值3,$\therefore$铅球飞行至水平距离4m时,达到最大高度为3m,故②正确;当$y = 0$时,$- \frac{1}{12} x^2 + \frac{2}{3} x + \frac{5}{3} = 0$,解得$x_1 = 10$,$x_2 = -2$(舍去),$\therefore$铅球落地时的水平距离为10m,故③正确.故选D.

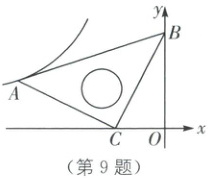
9. 在平面直角坐标系$xOy$ 中，将一块含有$45^{\circ}$角的直角三角板如图放置，直角顶点 C 的坐标为$(-1,0)$，顶点 B 的坐标为$(0,2)$，顶点 A 恰好落在第二象限的双曲线上，则该双曲线的表达式为 (A).

A.$y = -\frac{3}{x}$
B.$y = \frac{3}{x}$
C.$y = \frac{2}{x}$
D.$y = -\frac{2}{x}$

答案：
9.A [解析]本题考查了待定系数法求反比例函数的解析式、等腰三角形的性质、全等三角形的判定与性质.如图,过点$A$作$AD \perp x$轴,垂足为$D$,由题意可知,$\angle ADC = \angle COB = 90°$.$\because \angle ACB = 90°$,$\therefore \angle DAC + \angle ACD = 90°$,$\angle ACD + \angle BCO = 90°$,$\therefore \angle ACD = \angle CBO$.$\because AC = CB$,$\therefore \triangle ACD \cong \triangle CBO$,$\therefore AD = OC$,$CD = BO$.$\because$点$B$的坐标为$(0,2)$,点$C$的坐标为$(-1,0)$,$\therefore AD = 1$,$CD = 2$,$\therefore$点$A$的坐标为$(-3,1)$.设双曲线的函数表达式为$y = \frac{k}{x}$,将点$A$坐标代入可得$k = -3 × 1 = -3$,$\therefore$双曲线的函数表达式为$y = - \frac{3}{x}$.故选A.

10. 抛物线$y = ax^{2} + bx + c$的部分图象如图所示，顶点坐标为$(-1,-2)$，现有以下结论：①$abc ＜ 0$；②$3b + 2c ＞ 0$；③若 t 为任意实数，则有$a - bt ＜ at^{2} + bt$；④$4a(c + 2) = b^{2}$；⑤当图象经过点$(1,2)$时，方程$ax^{2} + bx + c - 2 = 0$的两根为$x_{1}$，$x_{2}(x_{1} ＜ x_{2})$，则$2x_{1} + 3x_{2} = 3$.其中正确的结论有 (C).

A.1 个
B.2 个
C.3 个
D.4 个

答案： 10.C [解析]本题考查了二次函数图象与系数的关系.$\because$抛物线开口向上,$\therefore a ＞ 0$.$\because$抛物线的顶点为$(-1,-2)$,$\therefore$抛物线的对称轴为直线$x = - \frac{b}{2a} = -1$,$\therefore b = 2a ＞ 0$.$\because$抛物线与$y$轴的交点在负半轴,$\therefore c ＜ 0$,$\therefore abc ＜ 0$,故①正确;$\because$当$x = 1$时,$y = a + b + c ＞ 0$,$a = \frac{1}{2} b$,$\therefore \frac{1}{2} b + b + c ＞ 0$,$\therefore \frac{3}{2} b + c ＞ 0$,故②正确;$\because$当$x = -1$时,$y$取最小值为$a - b + c$,$\therefore t$为任意实数时,$a - b + c \leq at^2 + bt + c$,即$a - bt \leq at^2 + b$,故③错误;$\because$抛物线的顶点为$(-1,-2)$,$\therefore \frac{4ac - b^2}{4a} = -2$,$\therefore 4ac - b^2 = -8a$,整理,得$4a(c + 2) = b^2$,故④正确;$\because$抛物线与直线$y = 2$的两个交点关于直线$x = -1$对称,图象经过点$(1,2)$,$\therefore$图象经过点$(-3,2)$,$\therefore$方程$ax^2 + bx + c - 2 = 0$的两个根为$x_1 = -3$,$x_2 = 1$,$\therefore 2x_1 + 3x_2 = 2 × (-3) + 3 × 1 = -3$,故⑤错误.故选C.

11. 把点$A(m,2)$向左平移 3 个单位得到点$B(6,2)$，则$m =$9

答案： 11.9 [解析]本题考查了点的平移.点$A(m,2)$向左平移3个单位得到点$B(6,2)$,$\therefore$依据平移规律“左减右加”得$m - 3 = 6$,解得$m = 9$.

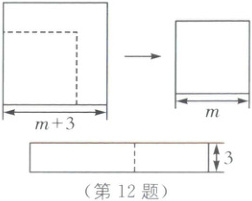
12. “这么近，那么美，周末到河北”——提到河北，很多人都会想到这句广告语，也正因为这条广告，河北越来越成为人们假日旅游的首选地.为了增强游客的游玩体验、展现景区文化特色，某景区欲制作一个长方形牌匾.如图，将一块边长为$(m + 3)$米的正方形铁片减去一个边长为 m 米的正方形后，剩余部分即可剪拼成一个长方形牌匾，若该牌匾一边长为 3 米，则其邻边长为$(2m + 3)$米(用含 m 的代数式表示).

答案： 12.$(2m + 3)$米 [解析]本题考查了整式的加减.依题意可知,剩余部分面积为$(m + 3)^2 - m^2 = m^2 + 6m + 9 - m^2 = 6m + 9$.$\because$拼成的矩形一边长为3米,$\therefore$另一边长是$(6m + 9) ÷ 3 = (2m + 3)$米.