2026年山东省中考试卷精选九年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年山东省中考试卷精选九年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
19. (本小题满分 8 分)
(1)计算:$(\frac{1}{2})^{-1}-\sqrt[3]{8}+|1-\sqrt{3}|+(2-\sqrt{3} \tan 60^{\circ})^{2025}$;
(2)解不等式组$\begin{cases} x+3>-2x \\ 2x-5 \leq 1 \end{cases}$,并把它的解集表示在数轴上.

(1)计算:$(\frac{1}{2})^{-1}-\sqrt[3]{8}+|1-\sqrt{3}|+(2-\sqrt{3} \tan 60^{\circ})^{2025}$;
(2)解不等式组$\begin{cases} x+3>-2x \\ 2x-5 \leq 1 \end{cases}$,并把它的解集表示在数轴上.

答案:
19.[解析]本题考查了实数的混合运算、一元一次不等式组的解法,解题的关键是掌握负整数指数幂的运算法则、二次根式的化简、特殊角的三角函数值、一元一次不等式组的解法.解:
(1)原式=2−2+$\sqrt{3}$−1+(2−3)²⁰²⁵=√3−1−1=√3−2.
(2)$\begin{cases} x+3>-2x,①\\\ 2x-5\leq 1,②\end{cases}$
解不等式①,得x>−1,
解不等式②,得x≤3,
∴不等式组的解集为−1<x≤3.不等式组的解集在数轴上表示如下.

19.[解析]本题考查了实数的混合运算、一元一次不等式组的解法,解题的关键是掌握负整数指数幂的运算法则、二次根式的化简、特殊角的三角函数值、一元一次不等式组的解法.解:
(1)原式=2−2+$\sqrt{3}$−1+(2−3)²⁰²⁵=√3−1−1=√3−2.
(2)$\begin{cases} x+3>-2x,①\\\ 2x-5\leq 1,②\end{cases}$
解不等式①,得x>−1,
解不等式②,得x≤3,
∴不等式组的解集为−1<x≤3.不等式组的解集在数轴上表示如下.

20. (本小题满分 8 分)东营市各县区积极创建全国义务教育城乡优质均衡发展县,为了解城乡教育质量发展情况,从农村和城区各抽取 1 所学校进行艺术抽测,每个学校均随机抽测了 10 名学生,数据分析如下.
[收集与整理]农村学校 10 名学生的艺术成绩(单位:分):64,74,78,82,84,86,86,92,96,98.
城区学校 10 名学生的艺术成绩(单位:分):62,70,79,83,85,87,87,90,97,100.
[描述与分析]城乡学生艺术成绩的平均数、中位数、众数和方差如下:
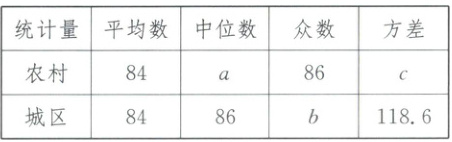
根据以上信息,回答下列问题:
(1)直接写出表格中 a,b,c 的值,a=
[迁移与应用](2)若从本次艺术成绩在 95 分以上的 4 名学生中,任意选择两名学生参加艺术展演,请用列表或画树状图的方法求出所选两名学生恰好都是城区学生的概率;
(3)请从以上统计量中,任选一个统计量,对这两所学校的艺术成绩进行对比分析,并对艺术教学提出一条合理化建议.
[收集与整理]农村学校 10 名学生的艺术成绩(单位:分):64,74,78,82,84,86,86,92,96,98.
城区学校 10 名学生的艺术成绩(单位:分):62,70,79,83,85,87,87,90,97,100.
[描述与分析]城乡学生艺术成绩的平均数、中位数、众数和方差如下:

根据以上信息,回答下列问题:
(1)直接写出表格中 a,b,c 的值,a=
85
,b=87
,c=95.2
;[迁移与应用](2)若从本次艺术成绩在 95 分以上的 4 名学生中,任意选择两名学生参加艺术展演,请用列表或画树状图的方法求出所选两名学生恰好都是城区学生的概率;
(3)请从以上统计量中,任选一个统计量,对这两所学校的艺术成绩进行对比分析,并对艺术教学提出一条合理化建议.
答案:
20.[解析]本题考查了中位数、众数、方差的定义、用样本估计总体、随机事件的概率计算.
解:
(1)85 87 95.2
(2)农村学校95分以上的学生有2人,分别记为A₁,A₂,城区学校95分以上的学生有2人,分别记为B₁,B₂,画树状图如下.
 总共有12种可能的结果,每种结果出现的可能性相同,其中所选两名学生恰好都是城区学生的结果有2种,
总共有12种可能的结果,每种结果出现的可能性相同,其中所选两名学生恰好都是城区学生的结果有2种,
∵P(所选两名学生恰好都是城区学生)=$\frac{2}{12}$=$\frac{1}{6}$.
(3)从平均数看,城区学校和农村学校的艺术成绩水平相同,建议继续保持城乡优质均衡发展.(答案不唯一)
20.[解析]本题考查了中位数、众数、方差的定义、用样本估计总体、随机事件的概率计算.
解:
(1)85 87 95.2
(2)农村学校95分以上的学生有2人,分别记为A₁,A₂,城区学校95分以上的学生有2人,分别记为B₁,B₂,画树状图如下.
 总共有12种可能的结果,每种结果出现的可能性相同,其中所选两名学生恰好都是城区学生的结果有2种,
总共有12种可能的结果,每种结果出现的可能性相同,其中所选两名学生恰好都是城区学生的结果有2种,∵P(所选两名学生恰好都是城区学生)=$\frac{2}{12}$=$\frac{1}{6}$.
(3)从平均数看,城区学校和农村学校的艺术成绩水平相同,建议继续保持城乡优质均衡发展.(答案不唯一)
查看更多完整答案,请扫码查看


