2026年山东省中考试卷精选九年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年山东省中考试卷精选九年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
22. (本小题满分 10 分)[活动背景]
如图,建筑物$AC,BD$的高度不可直接测量.为测量建筑物$AC,BD$的高度,技术员小李用皮尺测得$A,B$之间的水平距离为 150 m,用测角仪在$C$处测得点$D$的俯角为$35°$,测得点$B$的俯角为$43°$.
[问题解决]
(1)请运用技术员小李提供的数据求出建筑物$AC,BD$的高度;(结果保留整数,参考数据:$\sin 35°\approx0.57$,$\cos 35°\approx0.82$,$\tan 35°\approx0.70$,$\sin 43°\approx0.68$,$\cos 43°\approx0.73$,$\tan 43°\approx0.93$)
(2)请再设计一种测量建筑物$AC,BD$高度的方案(建筑物的宽度忽略不计),画出平面示意图,把应测数据在示意图中用字母标记出来,并用含字母的式子表示出建筑物$AC,BD$的高度.(可提供的测量工具:皮尺、测角仪)

如图,建筑物$AC,BD$的高度不可直接测量.为测量建筑物$AC,BD$的高度,技术员小李用皮尺测得$A,B$之间的水平距离为 150 m,用测角仪在$C$处测得点$D$的俯角为$35°$,测得点$B$的俯角为$43°$.
[问题解决]
(1)请运用技术员小李提供的数据求出建筑物$AC,BD$的高度;(结果保留整数,参考数据:$\sin 35°\approx0.57$,$\cos 35°\approx0.82$,$\tan 35°\approx0.70$,$\sin 43°\approx0.68$,$\cos 43°\approx0.73$,$\tan 43°\approx0.93$)
(2)请再设计一种测量建筑物$AC,BD$高度的方案(建筑物的宽度忽略不计),画出平面示意图,把应测数据在示意图中用字母标记出来,并用含字母的式子表示出建筑物$AC,BD$的高度.(可提供的测量工具:皮尺、测角仪)

答案:
22.[解析]本题考查了解直角三角形的应用——仰角俯角.解决此类问题要了解仰角和俯角的定义,找到与已知和未知相关联的直角三角形.当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另外,当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中的边角关系问题加以解决.
解:
(1)如图
(1),延长$BD$交过点$C$的水平线于点$E$,
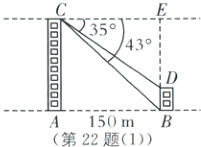
$\because\angle CAB=\angle ECA=\angle ABE=90^{\circ}$,
$\therefore$四边形$ABEC$为矩形,
$\therefore\angle BEC=90^{\circ}$,$CE=AB=150 m$,
$BE=AC$.
在$ Rt\triangle CDE$中,$\because\tan\angle DCE=\frac{DE}{CE}$,
$\therefore DE=150\tan35^{\circ}\approx105( m)$.
在$ Rt\triangle BCE$中,$\because\tan\angle BCE=\frac{BE}{CE}$,
$\therefore BE=150\tan43^{\circ}\approx140( m)$,
$\therefore AC=BE=140 m$,
$BD=BE-DE=35( m)$.
故建筑物$AC$的高度为$140 m$,建筑物$BD$的高度为$35 m$.
(2)为测量建筑物$AC$,$BD$的高度,用皮尺测得$A$,$B$之间的水平距离为$a m$,用测角仪在点$D$处测得点$A$的俯角为$\alpha$,测得点$C$的仰角为$\beta$,如图
(2),过点$D$的水平线交$AC$于点$E$,
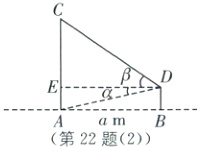
则$DE=AB=a m$,$BD=AE$,
在$ Rt\triangle ADE$中,
$\because\tan\angle ADE=\frac{AE}{DE}$,
$\therefore AE=a\tan\alpha( m)$,
$\therefore BD=AE=a\tan\alpha( m)$.
在$ Rt\triangle DEC$中,$\because\tan\angle CDE=\frac{CE}{DE}$,
$\therefore CE=a\tan\beta( m)$,
$\therefore AC=AE+CE=a(\tan\alpha+\tan\beta) m$,
即建筑物$AC$,$BD$的高度分别为$a\tan\alpha m$,$a(\tan\alpha+\tan\beta) m$.
解后反思 解直角三角形的应用是中考必考题,问题的特点是将实际生活中的物体,利用作辅助线构造直角三角形的方法解题,因为是实际应用问题,数据有时略大,计算要细心,要合理利用题目给定的数据,以勾股定理、三角函数为主要解题方法.解直角三角形的一般过程是:①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题);②根据题目已知特点选用适当的锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.
22.[解析]本题考查了解直角三角形的应用——仰角俯角.解决此类问题要了解仰角和俯角的定义,找到与已知和未知相关联的直角三角形.当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另外,当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中的边角关系问题加以解决.
解:
(1)如图
(1),延长$BD$交过点$C$的水平线于点$E$,

$\because\angle CAB=\angle ECA=\angle ABE=90^{\circ}$,
$\therefore$四边形$ABEC$为矩形,
$\therefore\angle BEC=90^{\circ}$,$CE=AB=150 m$,
$BE=AC$.
在$ Rt\triangle CDE$中,$\because\tan\angle DCE=\frac{DE}{CE}$,
$\therefore DE=150\tan35^{\circ}\approx105( m)$.
在$ Rt\triangle BCE$中,$\because\tan\angle BCE=\frac{BE}{CE}$,
$\therefore BE=150\tan43^{\circ}\approx140( m)$,
$\therefore AC=BE=140 m$,
$BD=BE-DE=35( m)$.
故建筑物$AC$的高度为$140 m$,建筑物$BD$的高度为$35 m$.
(2)为测量建筑物$AC$,$BD$的高度,用皮尺测得$A$,$B$之间的水平距离为$a m$,用测角仪在点$D$处测得点$A$的俯角为$\alpha$,测得点$C$的仰角为$\beta$,如图
(2),过点$D$的水平线交$AC$于点$E$,

则$DE=AB=a m$,$BD=AE$,
在$ Rt\triangle ADE$中,
$\because\tan\angle ADE=\frac{AE}{DE}$,
$\therefore AE=a\tan\alpha( m)$,
$\therefore BD=AE=a\tan\alpha( m)$.
在$ Rt\triangle DEC$中,$\because\tan\angle CDE=\frac{CE}{DE}$,
$\therefore CE=a\tan\beta( m)$,
$\therefore AC=AE+CE=a(\tan\alpha+\tan\beta) m$,
即建筑物$AC$,$BD$的高度分别为$a\tan\alpha m$,$a(\tan\alpha+\tan\beta) m$.
解后反思 解直角三角形的应用是中考必考题,问题的特点是将实际生活中的物体,利用作辅助线构造直角三角形的方法解题,因为是实际应用问题,数据有时略大,计算要细心,要合理利用题目给定的数据,以勾股定理、三角函数为主要解题方法.解直角三角形的一般过程是:①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题);②根据题目已知特点选用适当的锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.
23. (本小题满分 10 分)在平面直角坐标系$xOy$中,已知点$M(2,-3)$在抛物线$y=x^{2}-\frac{2}{3}mx-m$上.
(1)求抛物线的顶点坐标;
(2)点$N(a,b)$在抛物线上,若点$N$到$y$轴的距离小于 4,请直接写出$b$的取值范围;
(3)把直线$y=x$向下平移$n(n>0)$个单位长度后与抛物线的两个交点都在第四象限,求$n$的取值范围.
(1)求抛物线的顶点坐标;
(2)点$N(a,b)$在抛物线上,若点$N$到$y$轴的距离小于 4,请直接写出$b$的取值范围;
(3)把直线$y=x$向下平移$n(n>0)$个单位长度后与抛物线的两个交点都在第四象限,求$n$的取值范围.
答案:
23.[解析]本题主要考查了二次函数的性质、一次函数的图象与几何变换、二次函数的图象及二次函数图象上点的坐标特征,解题时熟练掌握并能灵活运用二次函数的性质是关键.
解:
(1)$\because$点$M(2,-3)$在抛物线$y=x^{2}-\frac{2}{3}mx-m$上,
$\therefore-3=4-\frac{2}{3}m×2-m$,$\therefore m=3$,
$\therefore y=x^{2}-\frac{2}{3}×3x-3$,
即$y=x^{2}-2x-3$,
$\therefore y=(x-1)^{2}-4$,
$\therefore$抛物线的顶点坐标为$(1,-4)$.
(2)$\because$点$N(a,b)$在抛物线上,点$N$到$y$轴的距离小于$4$,
$\therefore-4<a<4$.
$\because y=(x-1)^{2}-4$,
$\therefore$当$x=-4$时,$y=21$;当$x=1$时,$y$取最小值为$-4$;当$x=4$时,$y=5$,
$\therefore-4\leqslant b<21$.
(3)$\because$直线$y=x$向下平移$n(n>0)$个单位长度,
$\therefore$平移后直线为$y=x-n$.
如图,在平面直角坐标系中作出二次函数$y=x^{2}-2x-3$与直线$y=x-n$的图象.
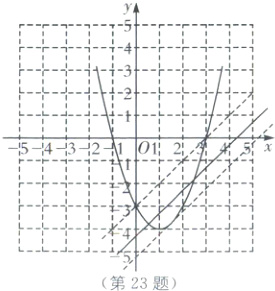
当$y=x-n$过点$(0,-3)$时,
则$-3=0-n$,$\therefore n=3$.
当$y=x-n$与$y=x^{2}-2x-3$有且仅有一个交点时,
方程$x^{2}-2x-3=x-n$有两个相等的实数根,即方程$x^{2}-3x-3+n=0$有两个相等的实数根,
$\therefore\Delta=9-4(-3+n)=0$,
$\therefore n=\frac{21}{4}$.
又直线$y=x$向下平移$n(n>0)$个单位长度后与抛物线的两个交点都在第四象限,
$\therefore$结合图象可得$3<n<\frac{21}{4}$.
23.[解析]本题主要考查了二次函数的性质、一次函数的图象与几何变换、二次函数的图象及二次函数图象上点的坐标特征,解题时熟练掌握并能灵活运用二次函数的性质是关键.
解:
(1)$\because$点$M(2,-3)$在抛物线$y=x^{2}-\frac{2}{3}mx-m$上,
$\therefore-3=4-\frac{2}{3}m×2-m$,$\therefore m=3$,
$\therefore y=x^{2}-\frac{2}{3}×3x-3$,
即$y=x^{2}-2x-3$,
$\therefore y=(x-1)^{2}-4$,
$\therefore$抛物线的顶点坐标为$(1,-4)$.
(2)$\because$点$N(a,b)$在抛物线上,点$N$到$y$轴的距离小于$4$,
$\therefore-4<a<4$.
$\because y=(x-1)^{2}-4$,
$\therefore$当$x=-4$时,$y=21$;当$x=1$时,$y$取最小值为$-4$;当$x=4$时,$y=5$,
$\therefore-4\leqslant b<21$.
(3)$\because$直线$y=x$向下平移$n(n>0)$个单位长度,
$\therefore$平移后直线为$y=x-n$.
如图,在平面直角坐标系中作出二次函数$y=x^{2}-2x-3$与直线$y=x-n$的图象.

当$y=x-n$过点$(0,-3)$时,
则$-3=0-n$,$\therefore n=3$.
当$y=x-n$与$y=x^{2}-2x-3$有且仅有一个交点时,
方程$x^{2}-2x-3=x-n$有两个相等的实数根,即方程$x^{2}-3x-3+n=0$有两个相等的实数根,
$\therefore\Delta=9-4(-3+n)=0$,
$\therefore n=\frac{21}{4}$.
又直线$y=x$向下平移$n(n>0)$个单位长度后与抛物线的两个交点都在第四象限,
$\therefore$结合图象可得$3<n<\frac{21}{4}$.
查看更多完整答案,请扫码查看


